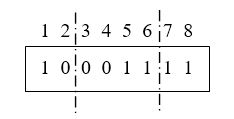شما اینجا هستید:  
  1. خانه
  2. عناوین مطالب
  3. رشته های دانشگاهی
  4. ژنتیک
  5. الگوریتم ژنتیک |عملگرهای الگوریتم ژنتیک | الگوریتم ژنتیک در بهینه سازی کاربرد الگوریتم ژنتیک | الگوریتم ژنتیک در هوش مصنوعی

الگوریتم ژنتیک |عملگرهای الگوریتم ژنتیک | الگوریتم ژنتیک در بهینه سازی کاربرد الگوریتم ژنتیک | الگوریتم ژنتیک در هوش مصنوعی

 

مطالب مرتبط:

 

الگوریتم های ژنتیک

 ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 

تکامل بیولوژیکی

در حدود سال های 1850 گریگور مندل[1] تئوری خویش مبنی بر تعریف ژن ها[2]  بنا نهاد. ژنها عملاً کدهای اطلاعاتی هستند که در بدن موجودات زنده بطور لایتغیر وجود دارند. هر ژن یک عامل تعیین خصوصیت ویژه‌ای از موجود زنده می‌باشد. مجموعه کامل ژن ها توصیف‌کننده مشخصات و عوارض بدن موجود زنده می‌باشد. این فرضیه موسوم به تئوری ژنتیک[3]  می‌باشد. ژن ها به طور عملی توسط ملکول های بسیار پیچیده ای به نام DNA و یا کروموزم[4]  کد شده‌اند. هر سلول در بدن یک ارگانیسم زنده یک کپی از همه کرموزم‌های مختلف را در خود دارد. در نتیجه هر سلول یک نمونه کامل اطلاعاتی از کل ارگانیزم را با خود حمل می‌کند. در طول رشد یا تکامل یک ارگانیسم، ملکولهای DNA برای کپی برداری (توارث) و انتقال اطلاعات از سلول والد یا سلول های والدین به سلول های جدیدالولادة استفاده می‌شوند.

چند سال بعد از ارائه تئوری ژنتیک، چارلز داروین[5]  در سال 1859، نظریه " منشاء انواع"[6]  را منتشر نمود. در این تئوری او به شرح و بسط نحوه تکامل موجودات زنده در قالب یک پدیده طبیعی می پردازد. تئوری ژنتیک مندل می‌توانست کمک بزرگی به داروین بنماید، ولی متأسفانه داروین از مفاد آن بی‌اطلاع بود. به هر حال، یک مشخصه مهم تئوری، تفوق بیشتر و شانس بقای انواع موجودات زنده قویتر یا سازگارتر با محیط، در طول زندگی و حتی نسل های بعدی می باشند. به عبارت ساده، قوی‌بنیه‌ها و سازگارترها زنده می‌مانند و این ویژگی را به فرزندان خود منتقل می‌کنند. داروین به این مسئله، عبارت و اصطلاح " انتخاب طبیعی"[7]  اطلاق می‌کند. بدین ترتیب، یک رشد تکاملی سریع از موجوداتی خواهیم داشت که بهتر از والدین و نسل های قبل‌ترشان با محیط خودشان تعامل داشته و خو می‌گیرند [ 2 ، 1].

 

تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی

در بسیاری از راه‌حل‌های مهندسی برای مسائل علمی و عملی، استفاده از سینرژیسم و نوعی ساببرنتیک متداول گردیده است. از بخش سخت‌افزاری می‌توان از پرواز سنجاقک برای پرواز هلی‌کوپتر ایده گرفت یا بر اثر مشاهده و آزمایشات تجربی روی پرواز کور (!) خفاش‌ها به سنتز و طراحی و ساخت رادار پرداخت. در بخش نرم‌افزاری نیز می‌توان به نوعی از تناظر و آنالوژی شعور جاری در طبیعت بهره گرفت. یک مورد از استفاده هوشمندانه از این دست، طرح و حل مسائل بهینه‌سازی مهندسی با آنالوژی انتخاب طبیعی می‌باشد.

معمولا در اثر مشاهده قوانین طبیعی، دو دیدگاه متصور و سپس متصدق می‌شود. یکی فرضیه‌سازی ( در باره عملکرد، منشاء پیدایش و کشف راز آفرینش) و دیگری تعمیم‌دادن به عوالم و افکار دیگر از کانال برقراری آنالوژی و تناظر مفهومی بین دو سیستم فکری جاری متناظر. به‌طور مثال تنوع و تکثر ارگانیسم‌های مختلف بسیار اعجاب‌انگیز و قطعا سوال‌برانگیزست. در یک نگاه دیگر، آگاهی از سطح و میزان پیچیدگی متفاوت در خود افراد آن جامعه نباتی یا حیوانی می‌باشد. حال سوال اینجاست، اینها چگونه بوجود آمده‌اند، اصلا چرا اینطوریست؟ شایان ذکرست که بخش بزرگی از علوم مهندسی شارح و مقلد «چگونگی» کارکرد این سیستم‌های زنده می‌باشد، در حالیکه حوزه بحث ما در این بخش، «دانش چرایی» است. این امید را داریم که با فهم و تحلیل این «چرایی»ها، به کپی‌برداری انتزاعی و سپس به تصرف مبادی و ارکان آن برای تامین آبجکتیوهای مهندسی مسئله خودمان (بهینه‌سازی) بپردازیم. به بیان روشن‌تر، وضع موجود را حاصل تکرارها، اصطکاکات و تعامل انواع و اقسام نیروهای معلوم و مجهول بدانیم ولی آن را در قالب یک نبرد و تنازع بقا بدانیم. تابع هدف نیز نوعی خودخواهی فردی و/یا جمعی می‌باشد، یعنی (به‌زبان کیفی) «زنده‌ماندن». هر که برازنده‌تر، سازگارتر و قوی‌تر باشد، از اقبال بیشتری برای بقا و زنده‌ماندن برخوردارست. مسئله کمّی‌کردن این درجه برازندگی که از خواص و مشخصه‌های علوم جدیده مهندسی است، یک امر پسینی است و بعدا اتفاق می‌افتد. عجالتا در مقام برقراری یک ساختار ذهنی و تناظری پایه‌ای هستیم. فرآیند تکامل نیز متکی به موتور و مکانیسمی است که با تقریب مشخصه‌های خاصی از تیپ افراد، آنها را تطبیقی‌تر، سازگارتر و جورتر می‌سازد. خود محیط و اصطکاکات موجود اعم از عامل حرکت و مانع پیشرفت به‌منزله همان قیود در مسائل بهینه‌سازی هستند.

 

ترمینولوژی فرآیند تکامل بیولوژیکی

برای شروع بحث راجع به نحوه جمع‌شدن این همه موجود زنده در حال تعامل و به‌خصوص نحوه تکامل آن باید دو جزء اصلی و مفهومی را مورد مطالعه قرار دهیم: علم ژنتیک و مفهوم تکامل. بیولوژیست‌های مدرن فرضیه‌ای دارند مبنی بر اینکه چگونه انتخاب طبیعی برگزار یا برقرار می‌گردد! و آن به‌طور خلاصه و ساده اینست که «تکامل از کانال سنتز ژنتیک می‌گذرد». قبل از جراحی این مفهوم لازمست موضع خودمان را در برابر دو دیدگاه تکامل ماکروسکوپی و میکروسکوپی بیان کنیم. مفاهیم تکامل کلان یا ماکروسکوپیک به توضیح و تبیین نظریه انقسام گروه‌ها و جمعیت‌های موجودات و ارگانیسم‌های زنده می‌پردازد، حال آنکه تکامل خُرد یا میکروسکوپی ، به خصوصیات داخلی و ویژگی‌های افراد فقط یک گروه خاص می‌پردازد. آنالوژی پیش‌گفته (بهینه‌سازی با تکامل انواع) در مقام تکامل خُرد می‌باشد و در این مقال، فقط به همان می‌پردازیم.

بدین ترتیب، باید به اصطلاحات و مفاهیم بیولوژیکی خُرد، یعنی وراثت (حفظ ویژگی‌ها) در سطح سلول بپردازیم. ژن‌های یک موجود زنده همیشه روی یک جفت کروموزم به فرم (مادیّ) شیمیایی دی‌اُکسی ریبونوکلئیک اسید[8] سوارست. این ملکول پیچیده (یعنی DNA) به فرم یک مارپیچ دوبله بوده و الگوی توالی ملکولی آن را می‌توان حمل بر نوعی بار اطلاعاتی یا کُدگذاری نمود که تعیین‌کننده توالی آنزیم‌ها و سایر پروتئین‌های آن موجود زنده می‌باشد. این توالی لایتغیر است و موسوم به کد ژنتیک[9] می‌باشد. هر سلول از موجود زنده شامل همان تعداد جفت کروموزم است. به‌طور مثال برای سلول‌های یک پشه این تعداد 6 تا می‌باشد، در حالی‌که 26 تا برای قورباغه، 46 تا برای نوع انسان و 94 تا برای ماهی حوض (ماهی قرمز) می‌باشد. ژن‌ها از نظر فانکشنال به دو شکل متفاوت ظاهر می‌شوند. هرکدام از این دو نوع مود موسوم به اَلل[10] می‌باشد. به‌طور مثال، یک نفر آدم ممکنست دارای اَلل چشم قهوه‌ای باشد و اَلل دیگر مربوط به چشم‌آبی‌بودن. ترکیب این اَلل‌ها روی کروموزم‌ها، ویژگی‌ها و مشخصه‌های فرد را معلوم می‌کنند. معمولا یکی از اَلل‌ها غالب و دیگری مغلوبست. به‌همین خاطر برای فرد چشم‌آبی مزبور معلوم می‌شود که اَلل چشم‌آبی‌بودن غالب بوده‌است و دیگری مغلوب. شایان ذکرست که هنگام وراثت هر دو اَلل منتقل می‌شوند ولی الزاما اَلل غالب در والد(ین)، همچنان در فرزند(ان) غالب باقی نمی‌ماند! (البتّه مگراینکه آن والد(ه) دیگر نیز دارای اَلل غالب چشم‌آبی باشد.)

به‌هرحال انتقال ویژگی‌های والدین به فرزندان (مساله وراثت) از طریق ژن‌ها (نظریه اول مندل) و آن ها نیز به‌نوبه خود از طریق اَلل‌ها صورت می‌گیرد. اگر اَلل‌های جفت ژن‌های والدین مثل هم باشند، آنها هموزیگوس[11] و درصورت مغایرت هتروزیگوس[12] هستند. در مورد رنگ چشم، ترکیب اَلل‌های قهوه‌ای-آبی یا آبی- قهوه‌ای هتروزیگوس و آبی-آبی  یا قهوه‌ای- قهوه ای  هموزیگوس هستند. ویژگی مشاهده شده (واقعیت) از فرزند مولود موسوم به فنوتایپ[13] بوده در حالیکه ترکیب محتمل و ممکن اَلل‌ها موسوم به ژنوتایپ[14] می‌باشد. یک تاس معمولی دارای ژنوتایپ شش وجهی (شش شماره‌ای) است در حالیکه برای تشخیص فنوتایپ (مصداق) آن باید تاس را پرتاب کنیم و ببینیم چه فنوتایپی می‌آید! برای مثالِ رنگ چشم، ممکنست والدین دارای فنوتایپ‌های چشم‌آبی وچشم‌قهوه‌ای باشند ولی دارای ژنوتایپ قهوه‌ای (فرم غالب ) باشند. ژنوتایپ را می توان از سهم یا درصد فنوتایپ های فرزندان (نسل‌های) بعدی (وحتی خود والدین) حدس زد! به این شکل که اگر فرزندی چشمان آبی داشت حتما والدین او دارای اَلل آبی (نه چشم آبی الزاما) بوده‌اند. نکته جالب اینست که ممکنست خود والدین هیچکدام چشمانِ آبی نداشته‌اند ولی در داشتن اَلل آبی آنها مطمئنیم. به‌هرحال از آنجایی که فرزند مزبور یک هموزیگوس بوده است ( چون دارای دو اَلل آبی بوده است یا دارای اَلل غالب آبی بوده است که در اینصورت باید چشم یکی از والدین آبی بوده باشد باید والدین او هتروزیگوس بوده باشند یعنی هر کدام واجد حداقل دارای یک اَلل آبی بوده باشند. این نظریه دوم مِندل موسوم به جورکردن یا جور شدن مستقل[15] می‌باشد. بیان خلاصه آن بدین شرح است: وراثت یا انتقال هر اَلل (برای هر ویژگیِ ) والد به مولود مستقل از نوع یا مقدار اَلل‌های خصایص (ویژگی های) دیگر می باشد. به طور مثال رنگ چشم ربطی به چاقی یا لاغری فرد ندارد. برای فهم بیشتر و تبیین بهتر ترکیب ژن‌ها برای تولید فتوتایپ‌ها بهترست کمی راجع به تقسیم سلولی بحث کنیم. توالد، تکاثر یا تناسل در ارگانیسم‌های تک سلولی به صورت تقسیم سلولی (موسوم به میتوز[16])  انجام می‌شود. در حین عمل تقسیم میتوز که کروموزم به شکل مادیّ خود دقیقا کپی شده و به مولود منتقل می‌شود. در یک چنین ارگانیسم ساده‌ای فرزندان (دختران!) دقیقا مثل والده (مادرشان) و نه والدین خود هستند ودر نتیجه شانس بسیار کمی برای تکامل دارند. مساله تکامل در این نوع ارگانیسم‌های ساده فقط به شکل جهش[17] ظاهر می‌شوند و بروز می‌کنند.ارگانیسم‌های پیچیده‌تر روش مدرن‌تری برای انتقال ویژگی‌ها دارند و آن تناسل جنسیتی یا دو جنسی می‌باشد. از این رو به این نوع تقسیم سلولی (رشد یا تکامل) می‌گویند تقسیم میوز[18]. سلول جنسی تناسلی (معروف به گامت[19]) نصف تعداد کروموزم‌های سلول را دارد. به همین خاطر به گامت‌ها می‌گویند هاپلویید[20] یا نیمدار، در حالی‌که به خود سلول های بدن (اندام) می‌گویند دیپلویید[21]. فقط دیپلوییدها کپی یا پازل کامل کد ژنیتکی را در اختیار دارند .موقع تقسیم میوز، دیپلوییدها کروموزم‌های خود را نصف می‌کنند تا تولید گامت کنند. موقع تکثیر یا تناسل این گامت‌ها هستند که خود را تکثیر می‌کنند. سپس گامت‌های سلول مادر به گامت‌های سلول پدر وصل می‌شوند (بیان نحوه‌ی اتصال و نقطه اتصال در حوصله این بحث نیست). بدین ترتیب گامت‌های والدین بعد از تکثیر و اتصال از خود یک آرایش جفتی معروف به همولوگ[22] می‌گیرند. چون هر کروموزم یک همزاد از نظر شکل وطول خواهد داشت. محل اتصال همزادان یک نقطه رندام موسوم به کنیتوکور[23] می‌باشد. به هر حال، همانطور که پروسه تقسیم میوز پیش می‌رود نیمه سمت چپ کنیتوکورهای کروموزم مادر به نیمه سمت راست کنیتورهای کروموزم پدر متصل می‌شود و بالعکس. این فرآیند موسوم به تقاطع یا اشتراک[24] می‌باشد‌. سلول مولود دقیقا همان تعداد کروموزم دیپلویید را دارد و عملا اجازه می‌دهد ویژگی‌ها سلول پدر و مادر به سلول فرزند منتقل شده و مستعد بروزدادن تفاوت‌های ظاهر با پدر مادرش شود. به‌هرحال، اگر به دومین محور مفهومی پدیده انتخاب طبیعی، یعنی مسئله تکامل برگردیم، باید با پیشگام نظریه معروف تکامل، یعنی چارلز داروین شروع کنیم. او که به عنوان یک طبیعی‌دان به سفری در جزایر گالاپاگوس[25] رفته بود، نظریات خود را (نظریه تکامل داروین) در چهار گروه خلاصه کرد:

  • عاقبت گرگ‌زاده گرگ شود، یعنی فرزندان در بسیاری از خصوصیات فردی با والدینشان شریک یا مساوی هستند. بدین‌ترتیب یک جمعت (جامعه) پایدار می‌ماند!
  • هنگام گذران عمر یا انتقال نسلی به نسل دیگر، شاهد مغایرتها و تفاوتها در ویژگی‌های افراد آن جامعه هستیم.
  • تنها کسر کوچکی از مولودین می‌توانند به سن کامل رشد یا بلوغ برسند.
  • اینکه کدامیک از مولودین بقای طولانی‌تر خواهند داشت، وابسته به ویژگی‌های موروثی آنان می‌باشد.  

این چهار اصل موضوعه داروین، تشکیل نظریه تکامل را می‌دهند. دانشمندان بعدی، سعی کردند در قالب تئوری مدرن تکامل با زبان علوم ژنتیک، مبانی نظری این چهار اصل را تبیین کرده، بهبود داده یا تعمیم دهند.

به یک گروه که افراد تشکیل‌دهنده آن زوج خود را از همان مجموعه برای تناسل انتخاب می‌کنند، مصطلحا یک جمعیت[26] می‌گویند. تحت شرایط استاتیکی، ویژگی‌ها و مشخصه‌های جمعیت توسط قانون هاردی – وینبرگ[27] بیان می‌شود. این اصل می‌گوید فرکانس یا فراوانی وقوع ترکیبهای مختلف اَلل‌ها در جمعیت مزبور ثابت می‌ماند مگر اینکه اغتشاشی یا تغییری (به‌مفهوم فلسفی) رخ دهد. به‌عبارتی گرچه افراد (نگاه خُرد) از خود ویژگی‌های متفاوت و حتی مغایر نشان می‌دهند اما ویژگی‌های روح جمعی، به‌مفهوم آماری (نگاه کلان) ثابت می‌ماند. به‌هر حال، در نظام‌های طبیعی کمتر شاهد جمعیت‌های استاتیکی هستیم. در نتیجه فرکانس یا وقوع ترکیب‌های اَلل‌ها ثابت (استاتیک) نمانده و از یک خصیصه دینامیکی در حین تولید نسل‌های متوالی برخوردارست. این خصیصه دینامیکی مسمّا به اصطلاح تکامل است و موتور و نیروی محرکه این تکامل (خصیصه)، دارای چهار خاستگاه زیر می‌باشد:

  • ممکنست جهش رخ دهد، یعنی احتمال (غیرصفر) دارد که تغییری در مشخصه‌های یک ژن رخ دهد. جهش‌ها ممکنست منشاء داخلی یا خارجی (در تعامل با محیط) داشته‌باشند.
  • ممکنست جریان یا انتقال ژن[28] به‌واسطه معرفی افراد جدید برقرار شود.
  • احتمال دارد نشت یا تلفات ژنتیکی[29] به‌طور تصادفی رخ دهد. این بدان معنیست که در جمعیت‌های کوچک احتمال دارد (کاملا تصادفی) ترکیب اَلل‌های خاصی از چرخه تولد و تناسل خارج شوند (منقرض شوند).
  • انتخاب طبیعی[30] باعث برجسته‌کردن برخی خصوصیات می‌شود. این خصوصیات برجسته عامل و فاکتور مهمی در بقاء یا اخذ بیشترین برازندگی افراد واجد آنها می‌باشند. به‌طور مثال، حیوانات چابک‌تر، در شکارکردن یا فرار از دست شکارچی، ورزیده‌تر و آماده‌ترند. در نتیجه بیشتر عمر (انتخاب طبیعی) می‌کنند و موقع توالد، فرزندان چابک بدنیا می‌آورند، چون دارای اَلل‌های چابکی و ورزیدگی نظیر بال‌های بلند، پاهای بادپیما و پنجه‌های قوی هستند.

 

الگوریتم ژنتیک

جان هلند[31]، دانشمند علوم کامپیوتر و روانشناس، مبدع شاخه ای از علوم کامپیوتربه نام «سیستم‌های تطبیقی پیچیده»[32] می‌باشد [3]. او در کتاب خود یک سیستم تطبیقی یا وفقی را چنین شرح می‌دهد که سیستم مربوطه به طور یکنواخت و پیوسته خودش را تغییر می‌دهد تا از محیط اطراف خود بهتر استفاده کند. هُلند در خلال توسعه تئوری خود برای سیستم‌های تطبیقی به شرح اپراتورهای ژنتیک[33] برای تغییر حالت سیستم می‌پردازد. گر چه کتاب هُلند، اختصاصاً برای سیستم‌های تطبیقی نگاشته شده‌است ولی یک مشخصه بسیار مهم دارد و آن ابداع و معرفی الگوریتم ژنتیک می‌باشد.

ژنتیک بیولوژیکی- بسیاری از اصطلاحات و ترمینولوژی الگوریتم ژنتیک برخاسته از پدیده های بیولوژیکی می باشد. فهم بسیاری از این پدیده‌های دیگر، می‌تواند کمک بزرگی به فهم، تعمیم یا بهبود الگوریتم‌های موجود ژنتیک نماید. به هر موجودی که قابلیت تکثیر، ترمیم و مرگ دارد، موجود زنده[34]  اطلاق می‌کنیم. به مجموعه‌ای از موجودات زنده از یک نژاد[35]  خاص در یک اقلیم[36]  خاص را جمعیت  می‌نامیم. هر موجود زنده در یک جمعیت، موسوم به فرد[37] می‌باشد. هر فرد بطور مقتضی با کدهای مدفون در آن، موسوم به کروموزوم‌ها  رشد می‌کند و بقاء دارد یا زندگی می‌کند. کروموزوم ها معرف مشخصه‌های طبیعی یک فرد هستند. به مجموعه کروموزوم های یک فرد، ژنوم یا ژنوتایپ  می‌گویند، چون معرفه ذات[38]  و نوع[39] فرد هستند. در حالیکه به شیوه رشد یا بقاء، فنو تایپ  می‌گویند، چون مفهومی اکتسابی و از جنس پدیده‌شناختی[40] و وقوعی می‌باشد.

هر کروموزوم شامل بیت[41] های اطلاعاتی و تکه‌های رقومی هستند. هر کدام از این تکه‌ها موسوم به ژن  می‌باشند. در یک بیان تناظری، نسبت مادی ژن به کروموزوم به فرد مثل نسبت معنوی حرف به کلمه به جمله می‌باشد.

هر ژن می‌تواند مقادیری را اختیار کند و هر مقدار ممکن موسوم به یک اَلل  می‌باشد. در صورتی که ژن کد باینری باشد، آنگاه دو اَلل بیشتر نداریم، یکی مقدار صفر (0) و دیگری مقدار (1) و موقعیت یک ژن در کروموزوم مربوطه معروف به مکان یا موقعیت[42] می‌باشد.

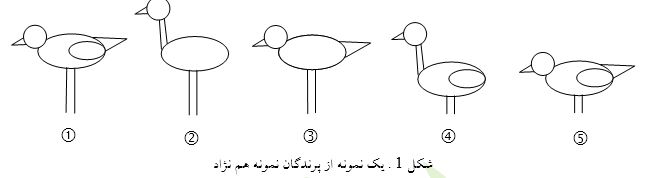
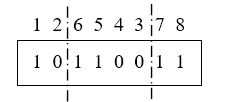
جهت تفهیم و تعمیق اصطلاحات یادشده، یک مجموعه ساده پنج عضوی از پرندگان یک نژاد خاص (مثلاً اُردک ها) را در نظر بگیرید.

 

 ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 

 

شکل1، جمعیت پنج نفره با خصوصیات مختلف را نشان می‌دهد. باید دقت نمود که محض سادگی فعلاً فنوتایپ ( یعنی خواص اکتسابی و انتخابی طبیعی ) پرندگان نشان داده شده است. به عبارتی گر چه پرندگان مورد نظر از یک نژاد هستند و به مفهوم نژادی با هم برابر هستند ( تعداد ژن‌های کروموزوم موجد آنها با هم برابرند و دارای ژنوتایپ یا ژنوم یکسان هستند) ولی از نظر ظاهری با هم تفاوت دارند، یعنی دارای فنو‌تایپ‌های مختلف هستند. همین که یک پرنده دارای ساق های بلند است ولی دیگری از همان نژاد دارای ساق‌های کوتاه هست نشان از تکثر و تنوع فنوتایپ دارد. علت این تکثر و تنوع، خواه در راستای صدق نظریه داروین ( انتخاب طبیعی ) باشد یا هر نظریه دیگر، به هر حال یک مفهوم و معلول یا حتی مدلول پدیده‌شناختی می‌باشد، لذا می‌گوییم فنوتایپ‌های مختلف یا انواع مختلف یک جمعیت هم نژاد ( یا هم ژنوم). به اختلاف مفهومی فنوتایپ و ژنوتایپ باز هم دقت کنید. فنوتایپ یک مفهوم اکتسابی و واقعیست در حالیکه ژنوتایپ یک مفهوم ذاتی و حقیقی می باشد. بطور مثال فنوتایپ ‚ و„ را در نظر بگیرید. هر دو بدون دُم هستند. شاید یک دُمش را در حین پرواز از دست داده است و دیگری در یک سانحه دام‌گذاری(!) . به هر حال وقوعی و حادثه‌ای بوده است ولی از آن طرف در لوح محفوظ (حقیقت) ژنوم پرنده، « دُم» در نظر گرفته شده‌است خواه در عمل (واقعیت) وجود داشته باشد یا نداشته باشد. بطور خلاصه، ژنوتایپ‌ها، معرف ساختار و تعداد ژن‌های کروموزوم هستند، در حالیکه فنوتایپ‌ها، معرف مقادیر عددی ژن ها ( بیت ها) هستند، علت تنوع ژنوتایپ‌ها، تعداد و ساختار مختلف کروموزوم‌هاست در حالی‌که علت تنوع فنوتایپ ها، مقادیر مختلف اَلل‌های یک ژنوتایپ است. برای مثالِ پرندگان، نژاد یا ژنوم یک پرنده نوعی، به صورت یک کروموزوم چهار ژنی ( ژن های « گردن»، « ساق»، « دام» و « بال» ) نشان داده می‌شود. یک فنوتایپ نمونه (مثلاً فنوتایپ „ در شکل1) به‌صورت «گردن‌دراز»–«ساق‌کوتاه»– «بدون دم»– « بالدار» نمایش داده می شود. به عبارتی اولاً) همه پرندگان دارای کروموزوم و ژنوتایپ چهار ژنی یکسان هستند، ثانیاً) ژن مربوط به ساق پا، می‌تواند فقط دو اَلل اختیار کند،  یکی«کوتاه» و دیگری «بلند» . اگر اَلل‌های ژن ساق پا می‌توانست سه مقدار «کوتاه»، «متوسط» و «بلند» را اختیار کند، آنگاه می‌توانستیم انتظار وجود سه فنوتایپ کاملاً مختلف (با مصدر صدور ژن ساق) را داشته باشیم و اگر بطور رقومی آن را بیان کنیم، باید ژن ساق را به صورت یک عدد تک رقمی در مبنای 3 بیان کنیم یا برای یکپارچگی آن را به صورت باینری (مبنای2) و شامل دو بیت نشان دهیم. در شکل2، فنوتایپ شماره 5 نشان داده شده است. فنوتایپ مربوطه دارای کروموزوم 4 بیتی می‌باشد چون مقدار هر بیت شامل فقط دو حالت است (بله یا خیر، Y یا N ). به تعریف ذوقی و سلیقه‌ای اَلل‌های هر ژن دقت کنید: بال دارد یا خیر؟، دُم دارد یا خیر؟، آیا دارای ساق بلند است؟، آیا دارای گردن دراز است؟ .

 

 ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

  

 حال به نحوه کمّی کردن یا کدکردن کروموزوم (ژنوتایپ) پرنده دقت کنید. « ژن در موقعیت1 (از سمت چپ) روی کروموزوم پرنده، سایز گردن را معلوم می کند». کمیت Y (یا 1)، اَلل گردن‌درازی است و کمیت N ( یا عدد 0 ) اَلل گردن‌کوتاهی است. بیان ژنتیک فنوتایپ … در جدول 1 نشان داده شده است.

 

فنوتایپ

اَلل

موقعیت

ژن

پرنده گردن کوتاه دارد

N

1

گردن درازی

پرنده ساق بلند نیست

N

2

ساق بلندی

پرنده دُم دارد

Y

3

دم

پرنده بالدار است

Y

4

 

جدول 1 . توصیف پرنده شماره … به بیان ژنتیک

 
 

بال

 

 

 

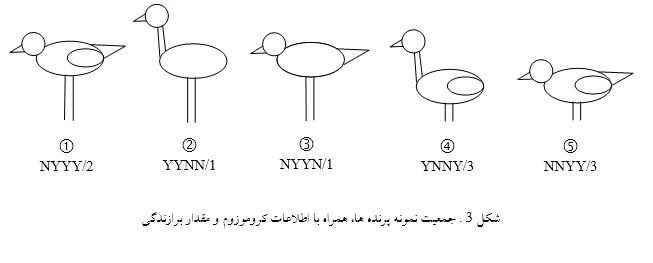
پس از معرفی الفباء و قاموس ژنتیک،  به شرح پروسه‌های ژنتیکی و تناظر تحولات بیولوژیکی با نظام مهندسی، جستجو و بهینه‌یابی می‌پردازیم. مطابق نظریه داروین، فنوتایپ یک پرنده، میزان اقبال یا شانس زنده ماندن او را تعیین می کند. به طور مثال اگر پرنده بالدار نباشد، در یافتن غذا برای خود و بچه هایش دچار مشکل می شود، چون شعاع مانور کمی دارد یا در هنگام خطر، محروم از شانس فرار از طریق پرواز است. همینطور دُم پرنده که تعادل یا عملکرد پروازی او را معیّن می‌کند. لذا دو ژن اخیر دارای ساق مثبت هستند، یعنی وجود بال و دُم هر کدام به نحوی شانس زنده‌ماندن را زیاد (ماگزیمم) می‌کنند. به طریق مشابه، ساق کوتاه نشان از آسیب‌پذیری کمتر دارد (به ویژه هنگام فرود) ولی از آنطرف ساق بلند و گردن بلند دستیابی به غذاهای دور از دسترس را آسان‌تر می‌کند. به هر حال، هر کدام از ژن‌ها به نوعی در شانس یا ماگزیمم‌سازی بقای نوع شرکت دارند، چه با ارزش مثبت و چه با ارزش منفی. برای مثال یاد شده، پرنده‌ای دارای بیشترین شانس بقاست که دارای گردنِ دراز، ساقِ کوتاه، دارای دم و بالدار باشد. به زبان ژنتیک کروموزم آن به صورت YNYY باشد ( این پرنده در شکل نشان داده نشده است ).

برای ورود به عالم مهندسی که سیطره کمّیت در آن جاریست، باید شانس بقاء را درجه‌بندی یا کمّی کنیم. این کار با قریحه و ذوق مهندسی در ارتباط تنگاتنگ است. یک شیوه معمول و متداول درجه‌بندی، مقایسه یا میزان نزدیکی با حالت ایده‌آل است. مثلاً برای مثالِ یاد شده این بخش، به ازای هر اَلل مشترک با حالت ایده‌آل، یک امتیاز به پرنده می‌دهیم تا میزان برازندگی[43] برای بقاء را رقومی و عددی کرده باشیم. بدین ترتیب، پرنده ایده‌آل (پرنده نوح!) دارای برازندگی 4 است. در شکل3، همان جمعیت قبلی ولی با کروموزم و تابع برازندگی معلوم دو فرد، نشان داده شده است.

 

 ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 حال به نحوه تکثیر پرندگان بپردازیم. اگر دو پرنده والدین یک پرنده جدید باشند، مطابق نظریه مندل آنگاه اَلل‌های فرزند، مخلوطی از اَلل‌های والدین خواهد بود. اختلاط اَلل‌های والدین به اصطلاح الگوریتم ژنتیک؛ «اپراتورهای ژنتیک» نامیده می‌شود. یک اپراتور ژنتیک از کروموزم‌های هر دوی والدین استفاده می‌کند تا کروموزم فرزند را حاصل کند. از آنجایی که مطابق نظریه داروین، تنها برازنده‌ترین افراد شانس بقاء و تکثیر دارند، لذا انتظار می‌رود با ترکیب و به کارگیری فرضیه توارث مِندل، فرزندان یا افراد نسل بعدی، اگر برازنده‌تر نیستند، حداقل به برازندگی نسل قبلی باشند.

فرض کنید پرنده های „ و … که برازنده‌ترین هستند (پس مُعمّرترین هستند و شانس توالد دارند)، با هم جفت شوند. از آنجایی که هر دوی والدین بالدار و پا کوتاه هستند، لذا فرزند آنها نیز بالدار و پا کوتاه می‌باشد به شرطی که جهش  رخ ندهد. به عبارتی فرزند خصائل (ژن) والدین خود را به طور عمده کسب می‌کند. به عبارت دقیق‌تر، مقدار برازندگی فرزند حداقل 2 می‌باشد. تمامی حالات ممکن توارث برای فرزند نسل بعدی (از فنوتایپ های „ و … ) در جدول2 آمده است. اگر هر ترکیب ممکن اَلل‌ها را با شانس مساوی در نظر بگیریم، 50% احتمال آن می‌رود که فرزند مولود (فنوتایپ نسل بعدی، متولد از والدین برتر) به برازندگی هر کدام از والدین باشد، 25% احتمال اینکه پرنده جدید، برازنده‌تر از هر کدام از والدین باشد و 25% احتمال آن هست پرنده جدید، کمتر از هر کدام از والدین برازنده باشد. همانطور که معلومست، نسل بعدی بطور متوسط برازنده‌تر از نسل قبل خواهد بود.

  

برازندگی

منشاء

کروموزوم

3

گردن از پرنده„، دم از پرنده „

YNNY

4

گردن از پرنده „، دم از پرنده …

YNYY

2

گردن از پرنده …، دم  از پرنده „

NNNY

3

گردن از پرنده ƒ، دم از پرنده …

NNYY

جدول 2 – حالات و ترکیب های محتمل برای فرزند پرندگان „ و ƒ

 

الگوریتم‌های ژنتیک –  اساس الگوریتم های ژنتیک مجموعه ای از جواب‌ها یا راه‌حل‌های ممکن می‌باشد. این مجموعه موسوم به جمعیت و هر حل ممکن معروف به فرد می‌باشد. در بسیاری از حالات، سایز جمعیت ثابت و فیکس می‌باشد.

هر فرد توسط یک ساختار[44]  متشکل از چند استرینگ[45]  بیان می‌شود. ساختار مربوطه، ژنوتایپ یا ژنوم عضو یا فرد نمونه از جمعیت می‌باشد، در حالیکه متناظراً نیز هر استرینگ در ژنوتایپ یک کروموزم نامیده می‌شود. غالباً و رایجاً ژنوتایپ مربوطه شامل فقط یک کرموزم (استرینگ) می‌باشد و در نتیجه کروموزم همان ژنوتایپ است. اگر کروموزم را هجا[46]  کنیم، عملاً بیان کمی کروموزم یا همان راه‌حل را معرفی کرده‌ایم. به عبارتی به فنوتایپ رسیده‌ایم. مجموعه تمامی راه‌حل‌های ممکن را فضای حل[47]  می‌نامند.

هر کروموزم (یا فرد یا جواب ممکن) شامل آرایه‌ای (استرینگ) از کاراکترهاست، هر کاراکتر بسته به موقعیتش در الگوی بیتی کروموزم و مقدار اَلل آن معنی خاصی دارد که هنگام فرمولاسیون مسأله تبیین می‌شود. ژن‌ها که سازنده کروموزم هستند، ممکنست تک‌کاراکتری (یا تک بیتی) باشند یا به صورت ترکیبی معنا و هجا شوند.

در کنار شاکله یک کرموزم، مقداری به نام برازندگی  به آن تخصیص می‌دهیم که بتوانیم به طور تمثیلی با قانون بقای انواع، عملکرد فرد (کروموزم) را نسبت به بقیه تمیز دهیم. مقدار برازندگی توسط ارزیابی یک تابع موسوم به تابع برازندگی (شیبه تابع هدف در مسائل بهینه‌یابی) تعیین می‌شود. برای فراخوانی تابع برازندگی از فنوتایپ فرد (به عنوان ورودی یا متغیر مستقل) استفاده می‌کنیم.

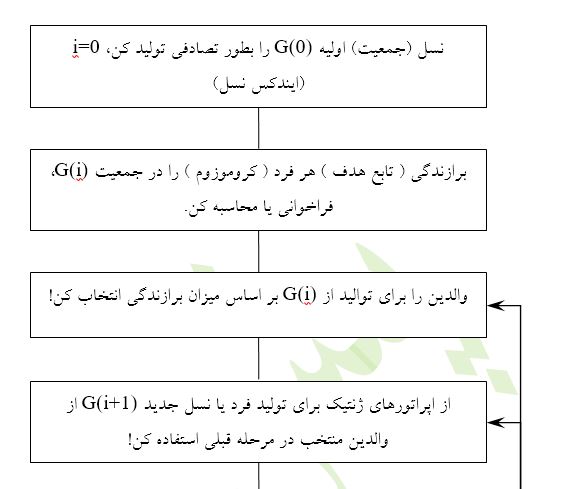
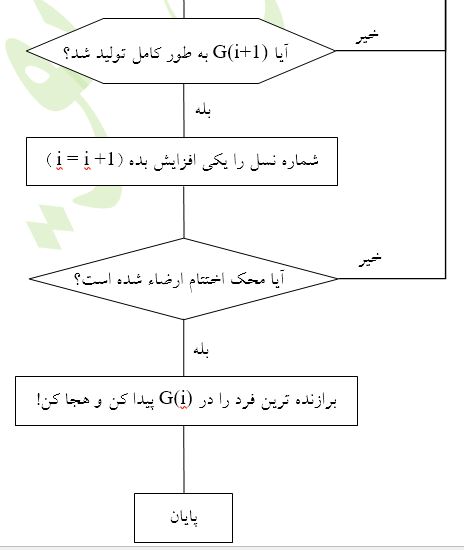
بر اساس برازندگی افراد جمعیت و استفاده از چند اُپراتور ژنتیک، به طور مصنوعی جمعیت جدید یا نسل جدید[48] را تولید می‌کنیم. چون نسل جدید، بطور متوسط دارای برازندگی بیشترست، لذا انتظار داریم که نسل بعدی بهتر یا برازنده‌تر از نسل قبلی باشد. یک الگوریتم ژنتیک مرتباً و مکرراً نسل‌های بهتر را تولید می‌کند تا با محک یک معیار اختتام، عملیات خاتمه یابد.

در شکل4 یک فلوچارت نوعی و متداول برای الگوریتم GA آمده‌است.

 ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 

اُپراتورهای ژنتيک - سه اُپراتور متداول ژنتيک عبارتند از بازتوليد[49]  ، قطع يا فصل[50]  و جهشی[51]. بازتوليد معادل مجازی يا متناظر نرم‌افزاری قانون بقای بهترين است. با اين اُپراتور يک فرد در نسل جاری به سادگی در نسل بعدی کپی می‌شود. در پروسه انتخاب والدين، معيار بالاترين يا بيشترين برازندگی می‌باشد، يعنی يک فرد با برازندگی بالا شانس بيشتری برای بقاء يا حضور در نسل بعدی را نسبت به فرد ديگری اما با برازندگی پايين دارد. لذا، اپراتور بازتوليد يا کپی، اين موضوع را تضمين يا اين قانون را تأييد می‌کند.

اُپراتور فصل، معادل مجازی يا متناظر نرم افزاری تقسيم يا تکثير دو جنسيتی می‌باشد. دو فرد از نسل قبلی به اقتضای برازندگی‌شان برای تکثير يا توليد دو فرد در نسل بعدی انتخاب می‌شوند. دو فرد قبلی موسوم به والدين و دو فرد نسل جديد موسوم به فرزندان می باشند. برای تکثير يک نقطه قطع[52]  به‌طور تصادفی در يکی از محل‌های کروموزوم انتخاب می‌شود. کروموزوم والدين در اين نقطه، به دو تکه تقسيم می‌شود. سپس اولين تکه‌ اولين کروموزوم به دومين تکه کروموزوم دومين والد يا والده اضافه می‌شود تا کروموزوم اولين فرزند درست شود. تکه‌های باقيمانده نيز به هم اضافه می‌شوند تا دومين فرزند به دنيای نسل جديد اضافه شود. حال اگر نياز به فقط يک فرد جديد باشد (کاهش جمعيت)، آنگاه فقط يکی از فرزندان به نسل جديد اضافه می‌شود.

به طور مثال اگر کروموزوم‌های والدين به‌ترتيب به صورت “ABCDE” و “abcde” باشند و نقطه قطع يا فصل بين ژن سوم و چهارم باشد، آنگاه کروموزوم فرزندان به صورت “ABCde” و “abcDE” می‌باشند. نکته قابل‌توجه آنست که تقسيم دو جنسيتی بيولوژيکی يا طبيعی با اين نوع تقسيم رياضی تفاوت ماهوی و کيفی دارد.

چون در اُپراتور اخيرالذکر نه مساله نرينگی – مادينگی مطرح است و نه نحوه ترکيب کروموزوم‌ها بدين صورت می‌باشد، اُپراتور جهش نيز معادل مجازی يا متناظر نرم افزاری موتاسيون طبيعی می‌باشد. بدين معنی که هر اَلل شانس اين را دارد که جهش کند يا به طور تصادفی مقدارش را عوض کند.

 

الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA )

الگوريتم‌های ساده ژنتيک رايج و متداول نوعاً دارای سايز جمعيتی ثابت، طول ثابت کروموزوم، تعداد توليد نسل معين و ثابت هستند و فقط از اُپراتورهای باز توليد، قطع و جهش استفاده می‌کنند. اين نوع الگوريتم‌ها معروف به الگوريتم‌های ژنتيک پايه (SGA) هستند. الگوريتم‌های SGA بيشتر مصرف آموزشی و انتقال مفهوم دارند تا يک کارکرد يا الگوريتم حرفه‌ای  [4]. اين الگوريتم‌ها در عمل نقاط ضعف زيادی دارند و لذا برای مقاصد حرفه ای بايد از واريانت‌های بهبود‌يافته آنها استفاده کرد.

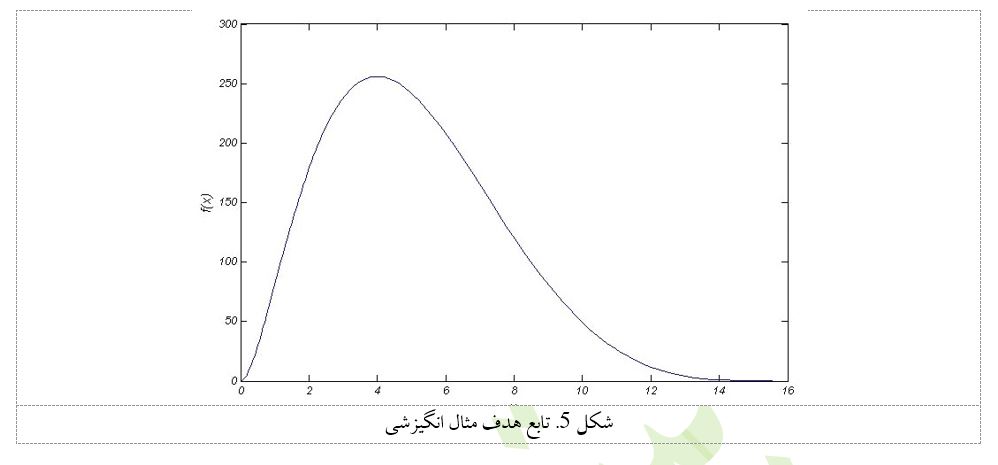
مثال انگيزشی - برای ورود به مطلب، ماکزيمم‌سازی تابع هدف ساده (تک متغيره، يونيمودال و نامقيد) زير را در نظر بگيريد:

ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 

مسأله کدينگ - برای ماکزيمم يابی f(x)  با استفاده از SGA، نيازمند نوعی کدينگ يا معادل يابی برای نمايش مقادير مختلف x داريم. در SGA نمايش به صورت باينری يا به اصطلاح کامپيوتری نمايش بيتی[53]  يا به اصطلاح رياضی، نمايش عددی در مبنای 2 را انتخاب می‌کنيم. يک مشکل مبنای 2 يا اعداد باينری، عدم توانايی آنها در نمايش صريح اعداد حقيقی[54]  می‌باشد.

در جبر اعداد باينری فقط می توان با شگرد خاصی، اعداد کسری و متجانس را نشان داد. در نتيجه مفهوم دقت[55]  و نمايش ماشينی اعداد مطرح شده است. به عبارت دقيق تر اگر عدد (کروموزوم) مورد نظر دارای L بيت يا رقم (در مبنای 2) يا طول L باشد، آنگاه کروموزوم (عدد باينری) مربوطه می تواند اعداد صحيح 0 تا  را نمايش دهد و برای نمايش کسری ( استفاده از resolution ) بايد گستره عدد مورد نظر را عاد کند:

(2)      

به طوری که x، نمايش عدد اعشاری ( البته به صورت کسری[56] )، R گستره مورد نظر ( برای مثال مربوطه، معادل 16 ) و B همان نمايش باينری يا عدد در مبنای 2 می‌باشد.

بدين ترتيب اگر بخواهيم يک عدد صحيح 6 رقمی ( L = 6 ) در مبنای 2 را نمايش دهيم، حداکثر تا عدد 1- 26 ( یا 63 ) می توان پيش رفت ولی اگر گستره نمايش اعداد را 16 - 0 در نظر بگيريم آنگاه می توان با دقت  ( تقسيم گستره به 64 قسمت ) اين فاصله را ريز کرد: يعنی اعداد 0، 4/1، 2/1، 4/3 و 1 و همينطور تا 2/151 و 4/153 را نمايش داد. به عبارت ساده، با تغيير دادن طول کروموزوم ( يعنی L ) می توان تولرانس يا دقت خط کش مساله را عوض کرد.

پارامترهای عملکرد –  برای مثال مورد نظر پارامترهای عملکرد زير را لحاظ يا طراحی می‌کنيم.

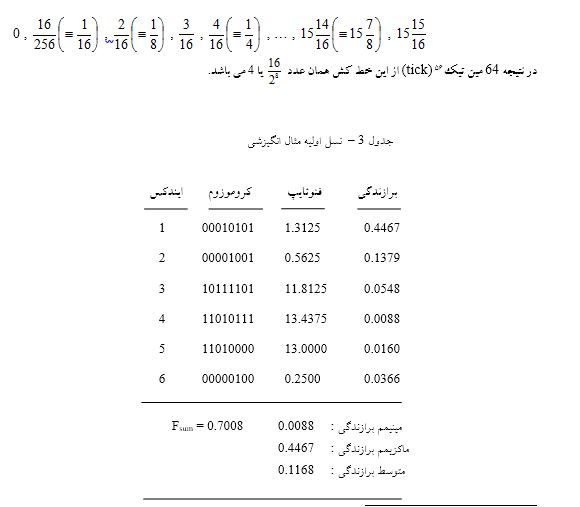
سايز جمعيت را معادل 6 در نظر می‌گيريم. اين عدد، مقدار کوچکی است. اصولا برای مساله يک متغيره توصيه می‌شود سايزهای بالای 100 انتخاب کنيم ولی برای سهولت تعقيب الگوريتم SGA، با همين عدد کوچک ادامه می‌دهيم. طول کروموزوم را معادل 8 ( يک بايت ) در نظر ‌گرفته و احتمال قطع را 7/0 در نظر می‌گيريم. اين بدان معنیست که شانس تولد يک فرد جديد ( در نسل بعدی ) از مکانيسم قطع، %70 می‌باشد. از طرفی چون فقط دو مکانيسم تکثير يا تولد داريم، لذا شانس تولد يک فرد جديد از طريق باز توليد معادل %30 خواهد بود. به اصطلاح مرسوم، نرخ جهش[57]  يا همان احتمال جهش را معادل 001/0 در نظر می گيريم. برای تابع هدف يا برازندگی مقدار  ( يعنی همان f(x)  ولی نرماليزه شده ) را در نظر می گيريم. لازم به‌ذکرست اين نحوه نرماليزاسيون هميشه ميسر نيست، چون مقدار ماگزيمم  را از قبل نمی‌دانيم. به هر حال، اين کار محض سهولت انجام شده و به کليت مساله لطمه‌ای نمی‌زند، دقت کنيد مقدار ماگزيمم برازندگی همان 1 است و مقدار متغير مستقل که تابع هدف ماگزيمم را می‌دهد  يا به زبان SGA، کروموزوم 01000000 يا عدد باينری 64 می‌باشد. دقت شود چون L را معادل 8 و گستره را 0-16 در نظر گرفته‌ايم، لذا دقت نمايش عدد حقيقی يا کوانتاهای خط‌کش متغير مستقل ( يعنی دامنه x )، معادل  يا 0.0625 می باشد، يعنی می‌توانيم دنباله زير را توليد کنيم:

 

ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 

 

 

اولین نسل -  جمعیت یا نسل اول بطور تصادفی انتخاب می‌شود، یعنی دو اَلل در کروموزوم توسط پرتاب سکه ( شیر یا خط )! معلوم می‌شود. برای این مثال خاص، فرض کنید به طور تصادفی 6 فرد جدید تولید کرده‌ایم. مقادیر نمونه در جدول 3، همراه با شاخص های مدیریت و تعقیب مسأله شامل مینیمم، ماگزیمم و متوسط برازندگی، نشان داده شده‌اند.

دومین نسل –  جمعیت و نسل دوم، مثل نسل اول بطور صریح تصادفاً تولید نمی‌شود، بلکه بطور ضمنی و البته هدفمند ولی تصادفی (!) تولید می‌شود.این نوع نظم تصادفی (!) را به‌نوعی یک نظم عالی تصور کرده و با الگوریتم تکاملی ژنتیک آن را تصدیق می‌کنیم. به هر حال با روش SGA، الگوریتم تولید نسل دوم را به شکل متعاقب زیر ادامه می‌دهیم.

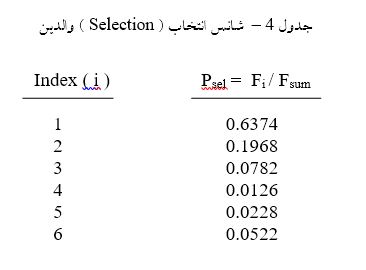
دو فرد متفاوت از نسل قبلی ( نسل اول ) انتخاب می‌کنیم. این انتخاب کاملاً تصادفی نیست بلکه بر اساس احتمال می‌باشد. احتمال شمارش شده (!) یا آماری باید با توجه به برازندگی بنا شود. در الگوریتم SGA این طور عمل می‌شود که اگر جمع مقادیر برازندگی افراد جمعیت حاضر را Fsum بنامیم آنگاه Fi / Fsum را مبنای شانس انتخاب برای والد بودن فرد i  با برازندگی Fi انتخاب کرده یا تخصیص داده ایم. بدین ترتیب فرد1 ( کروموزوم با ایندکس1) دارای احتمال والد بودن 0.4467 / ( 0.4467 + ... + 0.0366 ) یا 0.6374 خواهد بود. فرد دوم باید متفاوت از فرد اول باشد ولو اینکه دارای کروموزوم مساوی باشد.

در جدول4 مقادیر شانس انتخاب والدین برای تکثیر و گذر از نسل اول به نسل دوم نمایش داده شده است.

ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

لازم به ذکرست که انتخاب والدین به صورت قرعه‌کشی و تخصیص امتیاز به هر کروموزوم متناسب با توزیع احتمال آنها (جدول 4) انجام می‌شود. برای پیاده سازی می توان از قانون قرعه کشی که با احتمال و امتیاز وزن داده می‌شوند استفاده کرد. مثلاً برای مورد نمونه در جدول4، می توان یک آرایه 10000 تایی از اعداد صحیح در نظر گرفت، سپس 6374 تا عناصر این آرایه را بطور تصادفی با عدد 1 پر کرد، 1968 تا از عناصر اشغال نشده را با عدد 2 همین طور به ترتیب تا تمامی 10000 عنصر آن پر شود، حال می توان یک عدد کاملاً تصادفی صحیح بین 1 و 1000 را در نظر گرفته و در محل ایندکس تصادفی، مقدار عنصر آرایه را بازخوانی کرد. هر مقدار خوانده‌شده می‌شود ایندکس والد اول و بدیهیست با تجدید این کار، والد دوم نیز بدست می‌آید.

پس از انتخاب، نوبت به عملکرد اُپراتورهای ژنتیک می‌رسد. انتخاب اُپراتورها ( اُپراتور بازتولید یا قطع ) نیز تصادفی می‌باشد، البته به صورت قرعه یا همان توزیع احتمال. از آنجایی احتمال قطع در مثال نمونه معادل 7/0 است، لذا شانس انتخاب اپراتور قطع 70% و اپراتور بازتولید 30% است. برای پیاده‌سازی نیز شبیه انتخاب والدین که در بالا ذکر شد، عمل می‌کنیم. دقت کنید بحث شیر یا خط ( شانس 50 : 50 ) نیست بلکه مجدداً یک آرایه مثلاً 100 تایی در نظر گرفته و 70 تای آن را با عدد یا سمبل متناظر قطع پر می‌کنیم و 30 تای آن را با کاراکتر بازتولید. اگر بازتولید در این قرعه برنده شد، آنگاه با استفاده از نقطه قطع، دو فرزند جدید متولد می‌شوند و به جمعیت نسل دوم اضافه می‌گردند. لازم به ذکرست که نقطه قطع بطور تصادفی تولید می‌شود ولی نه با توزیع احتمال، بلکه هر محل قطع ( در اینجا 7 محل، چون کروموزوم 8 بیتی است ) از شانس مساوی 1/7 برای برنده شدن برخوردارست.

پروسه اخیرالذکر آنقدر تکرار می‌شود تا جمعیت نسل دوم ( بعدی )، هم اندازه جمعیت نسل اول ( قبلی ) شود. برای مثال انگیزشی این کار سه بار ( برای تولید فرد ، هر بار دو کروموزوم ) تکرار می‌شود. بعد از تکمیل نسل، شانس جهش را برای جمعیت جوان ( نسل دوم ) امتحان می‌کنیم. برای این کار هر اَلل را در هر کروموزوم با شانس جهش تعیین‌شده ( در اینجا 001/0 ) امتحان می‌کنیم. اگر در قرعه کشی 001/0 امتیازی، هر اَلل برنده شد، آنگاه مقدار اَلل به مقدار متضاد آن ( در اینجا به مقدار متناقض آن ) عوض می‌شود. مثلاً اگر مقدار 0 دارد به 1 تعویض می‌شود و بالعکس.

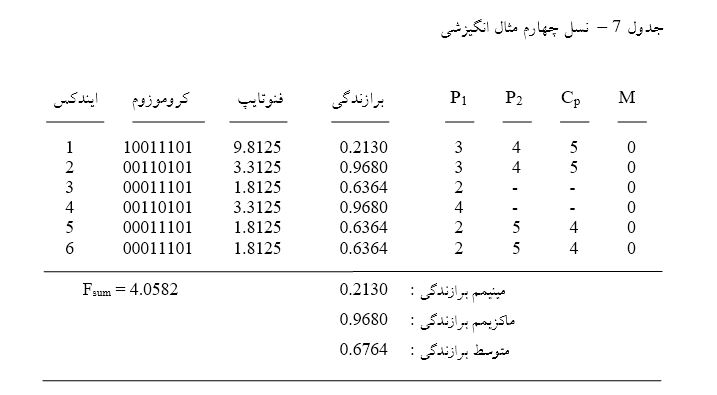
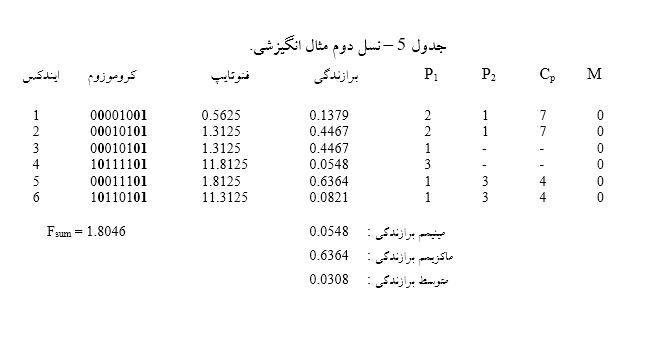
در جدول 5، نتیجه گذر از نسل اول به دوم نشان داده شده است. برای تعقیب بهتر آزمایش انجام شده، 4 ستون دیگر به جدول اصلی ( جدول 3 ، مشخصات جمعیت نسل اول ) اضافه شده است، ستون P1 و P2 ایندکس والدین فرد یا کروموزوم را نشان می‌دهند. در صورتی که خانه مربوط به ستون P2 خالی باشد بدین معنی است که اپراتور یوناری (غیر جفت یا تکی) بوده است که در اینجا تنها اپراتور تک آرکومان، همان اپراتور باز تولید است و ستون Cp محل تقاطع برای استفاده در اپراتور قطع می باشد، بدیهیست در صورت خالی بودن دو خانه در این ستون، بدین معنیست که اپراتور دیگر، یعنی اپراتور باز تولید برای تکثیر انتخاب شده است. ستون M نیز شانس یا اکتیو شدن عمل جهش می‌باشد. عدد صفر به معنی غیر فعال بودن یا صورت نگرفتن جهش می‌باشد.

یک نکته ظریف و قابل توجه این است که کروموزوم اول ( ایندکس1 ) در اکثر تولدها حضور داشته است. علت این است که شانس انتخاب کروموزوم 1 ( مقدار 74/63 % در جدول 4 ) برای والد بودن بسیار بالاست. مقام بعدی که دارای ثلث امتیاز یا شانس است، کروموزوم شماره ( ایندکس ) 2 می‌باشد. در طرف مقابل کروموزوم‌های 4 و 5 دارای کمترین احتمال ( به ترتیب 26/1 % و 28/2 % ) هستند، لذا اصلاً تأثیری در تولید نسل دوم نداشته‌اند.

نکته قابل توجه دیگر که البته قابل پیش بینی نیز بوده، بهترشدن تابع برازندگی است ( به مقادیر مینیمم، ماگزیمم و متوسط آن توجه کنید ) این بدان معنیست که نسل دوم بسیار بهتر و سازگارتر با محیط شده است! یا به مفهوم دنباله‌های ریاضی، نوعی همگرایی احساس یا استشمام می‌شود.

 ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSMنکته قابل تأمل آخر به شباهت الگویی کروموزوم ها می پردازیم. تمامی کروموزوم ها در نسل دوم، در اَلل های دوم، هفتم و هشتم مشترکند! ( در جدول بصورت پررنگ نمایش داده شده اند )

 

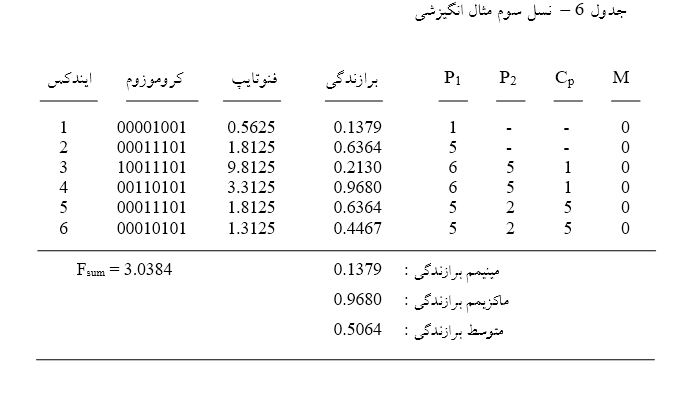
نسل های بعدی –  مشابه نسل دوم، برای نسل های بعدی نیز عملیات انتخاب والدین، اپراتور و احتمال جهش را تکرار می کنیم. نتایج در جداول 6 الی 11 نشان داده شده اند. دقت شود در نسل سوم، به یک جمعیت بسیار برازنده رسیده ایم.

 

 ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

  

جدول 8- نسل پنجم مثال انگيزشي

 

M

Cp

P2

P1

برازندگي

فنو تايپ

كروموزوم

ايندكس

0

1

2

5

0.9680

3.3125

00110101

1

0

1

2

5

0.6364

1.8125

00011101

2

0

4

2

5

0.4467

1.3125

00010101

3

0

4

2

5

0.9978

3.8125

00111101

4

0

-

-

3

0.6364

1.8125

00011101

5

0

-

-

6

0.6364

1.8125

00011101

6

 

مينيمم برازندگي : 0.4467                                                                                                                                                                                 

ماكزيمم برازندگي : 0.9978

متوسط برازندگي : 0.7203

 

جدول 9- نسل ششم مثال انگيزشي

 

M

Cp

P2

P1

برازندگي

فنو تايپ

كروموزوم

ايندكس

0

-

-

1

0.9680

3.3125

00110101

1

0

-

-

3

0.4467

1.3125

00010101

2

0

-

-

4

0.9978

3.8125

00111101

3

0

-

-

2

0.6364

1.8125

00011101

4

0

-

-

5

0.6364

1.8125

00011101

5

0

-

-

2

0.6364

1.8125

00011101

6

 

مينيمم برازندگي :0.4467                                                                                                                                                                                 

ماكزيمم برازندگي : 0.9978

متوسط برازندگي : 0.7203

 

جدول 10- نسل هفتم مثال انگيزشي

 

M

CP

P2

P1

برازندگي

فنو تايپ

كروموزوم

ايندكس

0

3

4

6

0.6364

1.8125

00011101

1

0

3

4

6

0.6364

1.8125

00011101

2

0

6

5

1

0.9680

3.3125

00110101

3

0

6

5

1

0.6364

1.8125

00011101

4

0

-

-

3

0.9978

1.8125

00111101

5

0

-

-

5

0.6364

1.8125

00011101

6

مينيمم برازندگي :0.6364                                                                                                                                                                                 

ماكزيمم برازندگي : 0.9978

متوسط برازندگي : 0.7519

 

جدول 11- نسل هشتم مثال انگيزشي

 

M

CP

P2

P1

برازندگي

فنو تايپ

كروموزوم

ايندكس

0

6

5

4

0.6364

1.8125

00011101

1

0

6

5

4

0.9978

3.8125

00111101

2

0

-

-

3

0.9680

3.3125

00110101

3

0

-

-

5

0.9978

3.8125

00111101

4

0

7

4

2

0.6364

1.8125

00011101

5

0

7

4

2

0.6364

1.8125

00011101

6

 

مينيمم برازندگي :0.6364                                                                                                                                                                                 

ماكزيمم برازندگي : 0.9978

متوسط برازندگي : 0.8121

 

اگر كروموزوم بسيار برازنده شماره 4 در نسل سوم (با برازندگي 0.9680 ) را مورد مداقه قرار دهيم، متوجه يك ويژگي متمايز در آن مي‌شويم. سه تا اَلل اول آن 001 است ( يعني اعداد يا فنوتايپ هاي بزرگتر از 2.0 و كوچكتر از 3.0 ). اين ويژگي، مزيتي يا نكته‌اي يا رابطه‌اي با ميزان برازندگي آن بايد داشته باشد. در حقيقت اگر مساله را تحليل كنيم در مي‌يابيم كه برازنده ترين كروموزوم كه با سه صفر (00011111) شروع مي‌شود، هنوز برازندگي كمتري نسبت به بدترين كروموزوم كه با 001 شروع مي‌شود (يعني 00100000) دارد. چون الگوريتم GA، متمايل به ايجاد نسل‌هاي بهتر مي‌باشد، لذا بايد انتظار وقوع بيشتر كروموزوم‌هايي را در نسل‌هاي آتي ( نسل چهارم، جدول 7 ) داشته باشيم كه با 001 شروع مي‌شوند.

 

ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 

در جدول 8، يعني نسل پنجم، مواجه با يك همگرايي سريع ( بهتر شدن نسل ) مي‌شويم. فقط چهار كروموزوم متفاوت داريم و تمامي كروموزوم ها در 6 محل ( از 8 محل ) با هم مشتركند. برازنده ترين فرد ( شماره4 درنسل پنجم ) در اين نسل، عملا بهترين آرايش بيتي را از نظر برازندگي دارد و چون 6 محل آن فيكس شده است، لذا اگر موتاسيون كمكي نكند، بعيد است ديگر بتوان فرد بهتري را پيدا كرد. اگر آزمايش را ادامه دهيم‌، همين انتظار نيز متحقق مي‌شود، نسل‌هاي ششم، هفتم و هشتم گرچه مينيمم و متوسط برازندگي اندكي بهتر دارند ولي سوپركروموزوم ( با برازندگي ماگزيمم 0.9978 ) هنوز همانست كه در نسل پنجم شاهد بوديم.

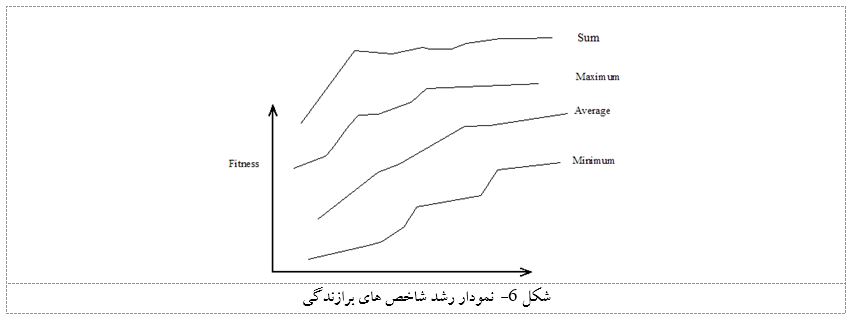
نمايش بهبود برازندگي - اگر به طور گرافيكي نحوه بهبود شاخص‌هاي برازندگي، يعني مينيمم، متوسط،  ماگزيمم و جمع برازندگي‌ها را قضاوت كنيم آنگاه به نظم تصادفي ولي هدفمند موجود در الگوريتم هاي GA پي مي‌بريم. براي مثال انگيزشي اين بخش ، نمودارهاي رشد برازندگي بر حسب نسل هاي توليد شده در شكل 6 نشان داده شده‌اند.

 

مسأله قياس

جهت بررسي و تجزيه و تحليل عملكرد الگوريتم هايGA ، جان هلند ( معروف به پدر الگوريتم ژنتيك ) مفهوم يا مسأله قياس[59] را معرفي كرد [3]. يك الگوي قياسي[60]  عملا يك مدل متشبّه[61] مي‌باشد، كه مثل برادران يك جمعيت تعريف مي شود. به بياني دقيق‌تر، يك الگو(ي قياسي) زيرمجموعه اي از استرينگ‌هاي (كروموزوم‌ها) هم‌طول مي‌‌باشد كه در موقعيت‌هاي (بيتي) خاص با هم مشتركند. يك الگو به صورت يك استرينگ هم‌طول با كروموزوم‌هاي جمعيت مي‌باشد ولي يك كاراكتر ( معمولا کاراکتر *) اضافه‌تر دارد، يعني در هر كجاي نقشه‌بيتي كروموزم، كاراكتر * درج شده‌باشد بدين معني است كه اَلل مربوطه هر مقدار ممكن مي‌باشد و مقدار آن مهم نيست. بطور مثال فرض كنيد يك استرينگ (كروموزم ) به طول 8 داريم و اَلل ها مقادير 0 يا 1 مي توانند داشته باشند. حال الگوي 000*01*0 معرف مجموعه زير مي‌باشد: (يعني در محل هاي چهارم و هفتم ، هر مقداري مي تواند بگيرد).

{  00010110، 000 0 01 10 ، 000 1 01 00 ، 000 0 01 00 }  000*01*0

الگوي 00****** ، يعني تمامي استرينگ هايي كه با دو صفر شروع مي شوند و الگوي ******** ، يعني مجموعه تمامي كروموزوم هاي جمعيت مورد مطالعه (!).

هُلند در مطالعات خود به اين نكته اشاره مي‌كند كه الگوريتم ژنتيك به اين خاطر درست كار مي‌كند كه برازندگي يك كروموزوم (يا استرينگ) فقط به خود فرد مربوط مي‌شود، بلكه به طور ضمني، روي همه مدل هاي متشابه نيز اثر مي‌گذارد. وقتي يك الگوي بيتي شامل برازنده‌ترين استرينگ‌ها مي‌باشد، الگوريتم ژنتيك اين مساله را در نسل‌هاي بعدي نيز لحاظ مي‌كند، يعني هر چه نسل عوض مي‌شود، استرينگ‌هاي متشابه بيشتري در جمعيت نسل‌ها ظاهر مي‌شوند.

فرض كنيد سايز جمعيت رابا n و طول هر كروموزوم را با L نمايش دهيم ، هر موقعيت در استرينگ را اگر با * جايگزين كنيم تا يك الگو توليد شود آنگاه الگو خواهيم داشت كه اعضاي آن جزء جمعيت خواهند بود. بنابراين كل جمعيت ، معادل  تاn الگو خواهد داشت.

به طور مثال استرينگ 10000010 كه جزء جمعيت باشد، عملا جزء زيرمجموعه الگوئي 1*****1* مي‌باشد ولي وقتي اپراتور قطع روي آن عمل مي‌كند، عملاً  شانس آن وجود دارد كه نقطه قطع بين دو تا 1 رخ دهد و عملا الگو شكسته شود. اگر يك الگو در گذر از نسلي به نسل ديگر، شكسته شود، آنگاه الگوريتم ژنتيك نتوانسته است بهره مناسبي از آن الگو ببرد ولو اينكه برازنده نيز باشد.

هُلند به محاسبه تعداد الگوهايي كه در الگوريتم ژنتيك پايه (SGA) قابل پردازش مناسب هستند پرداخت و  نشان داد كه از مرتبه[62]  مي باشند. اين مرتبه بسيار بزرگتر از تعداد يا سايز جمعيت يعني n مي باشد، لذا به نوعي يك تضمين براي كاركرد مناسب  SGA مي باشد.

تئوري قياس - اگر يك الگو مثل H داشته باشيم ، آنگاه مرتبه الگو كه با (H)O نمايش مي‌دهيم، به‌صورت تعداد محل ثابت و تعيين شده[63]  در الگوي H ، تعريف مي شود. طول مشخصه[64] يك الگو ( نمايش داده شده با) به صورت فاصله بين اولين و آخرين محل فيكس شده تعريف مي شود به طور مثال ، چون سه محل فيكس وجود دارد و، چون آخرين محل فيكس در ششمين نقطه و اولين محل فيكس شدن در محل دوم اتفاق مي افتند .

حضور يا رخداد[65]  يك الگوي خاص در جمعيت مورد مطالعه موقعي واقعيست كه اگر استرينگي در جمعيت وجود داشته باشد كه عضو زير مجموعه استرينگ‌هاي آن الگو باشد تعداد حضور يك الگو در يك جمعيت عملا همان تعداد استرينگ‌هايي مي‌باشد كه در عين حضور در جمعيت، عضو زيرمجموعه الگوي مربوطه باشند. برازندگي الگوي مزبور در آن جمعيت خاص مطابق برازندگي متوسط استرينگ‌هاي حاضر در جمعيت ولي متعلق به الگو تعريف مي‌شود. نكته قابل توجه اينست كه برازندگي يك الگو با زمان (تغيير نسل) تغيير مي‌كند.

به نسل اول مثال انگيزش بخش قبلي مراجعه كنيد. دو رخداد از الگوي ***101** در اين نسل وجود دارد، يعني كروموزوم هاي 1 و 4 برازندگي اين الگو، متوسط برازندگي دو كروموزوم 1 و 4 است يعني 2 = 0.2278/ ((0.4467+0.0088  نسل دوم : سه رخداد از اين الگو دارد ، يعني كروموزوم هاي 2 و 3 و 6 متوسط برازندگي الگو معادل متوسط برازندگي اين سه كروموزوم است ، يعني ( 0.4467+0.4467+0.0821 ) / 3 = 0.3252 .

فرض كنيد m(H,t) را تعداد حضور الگوي H در يك جمعيت نمونه در لحظه (نسل) t بناميم. همچنين f(H,t) را برازندگي H در نسل t در نظر بگيريد  را برازندگي متوسط جمعيت تعريف كنيد. هُلند نشان داد كه مينيمم تعداد رخداد يك الگو مثل H در نسل بعدي ( نسل  t+1) به صورت زير محاسبه مي شود 3] [ :

                (3)           

به طوريكه  طول كروموزوم،   احتمال قطع و   احتمال (شانس) جهش مي باشد.

رابطه بالا نشان مي دهد كه سرعت بهبود برازندگي به طور نمايي در نسل‌هاي متوالي بهبود پيدا مي‌كند، به شرطي كه اپراتورهاي پايه ژنتيك شامل بازتوليد، قطع و جهش باشد. اين قضيه معروف به قضيه قياس(تئوري) يا قضيه اساس الگوريتم هاي ژنتيك[66] مي‌باشد.

اگر به مثال انگيزشي بخش قبلي برگرديم، گفته شد كه انتظار مي‌رود كروموزوم هايي كه با 001 شروع مي‌شوند، در نسل‌هاي بعد ازنسل سوم نيز ظاهر شوند. با توجه به قضيه اساس الگوريتم‌هاي ژنتيك، اين پيش‌بيني يا انتظار درست از آب در مي‌آيد. براي استفاده از قضيه فوق‌الذكر، بايد تعداد تقريبي رخداد الگوي 001***** را در نسل بعدي ( نسل چهارم ) حساب كنيم :

 (4)          

يعني تعداد رخداد الگوي مزبور بايد حداقل 2 باشد. يك نكته را نيز نبايد ازنظر دور داشت وآن هم اين كه سايز جمعيتي مثال انگيزشي بسيار كوچكست و نتايج قضيه اساسي خيلي مشهود يا قابل توجه نيست.

يك استفاده كاربردي از قضيه اساسي، بحث مانيتورينگ و تعقيب برازندگي نسل حاضر يا عملكرد يك GA خاص مي‌باشد ولي آنچه بسيار مهم است، استفاده متعالي از اين قضيه است به طوريكه جوهره اصلي قضييه، راجع به توليد يا احتمال تولد افراد بسيار برازنده از روی بلوک‌های سازنده استرینگ‌های نمونه‌ای با طول کوتاه (یعنی الگوهای H) صحبت مي‌كند. حال ايده اينست كه به جاي تاكيد يا چانه زني توليد سوپركروموزوم ها از اول (استفاده از اپراتور قطع در GA)، آيا بهتر نيست از روي الگوهاي برازنده شروع كنيم؟!

نكات عملي پياده‌سازي GA - همانطوركه قبلا نيز ذكرشد، الگوريتم پايه‌اي ژنتيك (SGA) فقط محض سهولت فهم و تحليل كاركرد الگوريتم مطرح شد. براي كاربردهاي عملي و جدي بايد محورهايي از كاركردهاي GA را بهبود داد. به طور مثال، ممكنست با همگرايي بسيار سريع در همان چند نسل اول مواجه شويم واين برخلاف الگوريتم‌هاي جستجوي كلاسيك كه حساس به مقدار اوليه هستند خبر خوبي نيست! همچنين اُپراتورهاي قطع و بازتوليد الزاما براي همه مسائل مناسب نيستند و ساير اُپراتورهاي مقتضي را نيز بايد به كارگرفت. درادامه به چند تكنيك عملياتي براي بهره گيري بيشتر از GA مي‌پردازيم.

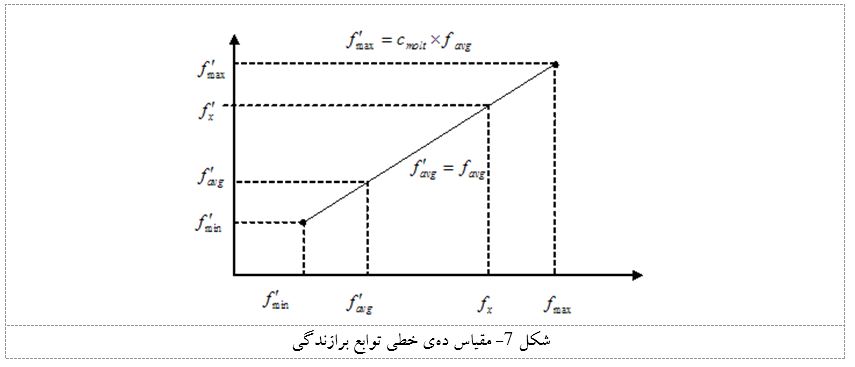
فرآيند مقياس دهي (Scaling) - همگرايي زودرس يكي از معايب عمده الگوريتم پايه SGA مي‌باشد. روش‌هاي زيادي براي جلوگيري از بروز اين پديده وجود دارد. يكي ازاين متدها، مقياس‌دهي مي‌باشد.

ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 

در مراحل ( نسل‌هاي ) اوليه يك GA، تعداد بسيار كمي از افراد از نظر برازندگي تمايل به غالب شدن در جمعيت دارند. در اين حالت، بايد به نحوي برازندگي آنها را كاهش دهيم تا افراد كمتر برازنده نيز شانس حضور در جمعيت يا نسل بعدي را داشته باشند. از طرفي ممكنست با تحقير سوپرمن‌ها، مسأله دوباره تكرار شود و لذا بايد به نحوي افراد خيلي ضعيف را به نوعي تعظيم كنيم. اين تحقير و تعظيم از نظر عددي، عملا به شكل مقياس‌دهي خطي است. براي عمليات مقياس‌دهي خطي، ابتدا ميزان و تابع برازندگي هر فرد را مثل هميشه محاسبه مي‌كنيم. اين اعداد موسوم به برازندگي‌هاي خام هستند. سپس متوسط()، ماگزيمم و مينيمم  برازندگي را حساب مي‌كنيم. با استفاده از اعداد محاسبه‌شده، مي‌توان برازندگي مقياس‌شده يا پردازش‌شده هر فرد را حساب نمود. شكل 7 ، به طور گرافيكي رابطه بين برازندگي‌هاي خام و برازندگي‌هاي پردازش‌شده يا مقياس‌شده را نشان مي‌دهد.

روابط خطي بين (بعنوان متغير مستقل) و (برازندگي مقياس‌شده، بعنوان متغير تابع) به صورت زير است :

براي محاسبه شيب (a) و عرض از مبدا (b) از دو رابطه زير استفاده مي‌كنيم :

(6)         

   (7)               

ثابت ، معمولا با تعداد كپي مورد انتظار از سوپر كروموزوم جمعيت در نسل بندي مقداردهي مي‌شود. به طور مثال اگر مقدار 2 را براي آن اختيار كنيم، يعني انتظار داريم كه برازنده ترين عضو جمعيت (نسل)، فقط دو بار شانس انتخاب‌شدن براي اپراتورهاي ژنتيك جهت توليد نسل بعدي را داشته‌باشد. از آنجائيكه برازندگي خام متوسط را معادل برازندگي مقياس‌دهي‌شده متوسط قرار داده‌ايم لذا، انتظار مي‌رود فرزندان افراد متوسط جمعيت حاضر نيز در نسل بعدي حضور داشته باشند. براي مشخصه‌سازي يك خط، نياز به دو نقطه مي‌باشد كه در بحث اخير، از تساوي دو متوسط برازندگي و متوسط ماكزيمم استفاده كرديم. گرچه مي‌توانستيم با دو مقدار مينيمم و ماگزيمم نيز به رابطه‌مندي خط برسيم ولي با هدف نهايي فرآيند مقياس‌دهي در تضاد و يا لااقل كنترل ناپذير بود. به‌هرحال، در اثر استفاده از روابط ( ( 6و (7) ، از رابطه زير استفاده مي‌كنيم:

(8)      

فرآيند انتخاب - نحوه و مكانيسم انتخاب در SGA دارای معايبي چند است. به طور مثال ممكنست برازنده‌ترين فرد در نسل بعدي حضور نداشته باشد(!). علت نيز معلومست، چون انتخاب شانسي است. به هر حال دو روش آلترناتيو نيز براي پرهيز ازاين نكته وجود دارد. انتخاب هميشگي زبدگان[67] به اين صورت عمل مي‌كند كه اين سوپركروموزوم هميشه در اپراتور بازتوليد لااقل يكبار شركت مي‌كند، يعني اگر هنگام توليد نسل جديد، اين سوپركروموزوم حضور نداشته باشد، هنگام توليد نسل بعدي كپي مي‌شود. انتخاب با متوسط آماري[68]  سعي مي‌كند با مينيمم كردن خطاي آماري هنگام فرآيند انتخاب، شانس حضور سوپركروموزوم ها در نسل بعدي افزايش يابد. با گذاشتن يك قيد ماگزيمم روي تعداد كپي افراد در نسل جديد با توجه به شانس افراد (برازندگي فرد تقسيم بر مجموع برازندگي) وقتي گرد مي‌شود اين مسأله متحقق مي‌شود.

جايگزيني و تعويض - به تجربه ثابت شده‌است كه نبايد كل جمعيت نسل قبل را حذف و با يك جمعيت جايگزين [69] كنيم. در عوض بايد بخشي از جمعيت قبلي را جايگزين كنيم. اين نكته منجر به مساله انتخاب فقط بخشي از نسل قبل براي توليد نسل جديد مي‌شود.

روش يا مفهوم ازدحام[70]  يك روش متداول و جاافتاده براي پياده‌سازي اين مكانيسم انتخاب مي‌باشد و نيازمند استفاده از دو پارامتر فاصله نسلي[71] و فاكتور ازدحام[72]  مي‌باشد.

فاصله نسلي نمايانگر ميزان بزرگي كسر جمعيت حاضر براي تعويض مي‌باشد. فاكتور ازدحام نيز نشان مي‌دهد  چند  فرد بايد مجموعه رفرنس براي انتخاب يك فرد را تشكيل دهند، يعني تعداد اعضاي مجموعه كانديداتوري براي انتخاب يك فرد جهت تعويض چه قدر است. به طور مثال اگر فاكتور ازدحام 2 باشد، آنگاه دو نفر به طور رندام براي كانديداتوري از نسل حاضر انتخاب مي‌شوند. يكي از اين دو نفر بايد براي تعويض با فرد جديدالولاده (حضور در نسل بعدي) انتخاب شود. معمولا آن فردي انتخاب مي‌شود كه بيشترين اختلاف بيتي يا كاراكتري (كمترين شباهت) را با فرد جديد دارد.

روش ديگر مكانيسم تعويض، مفهوم پيش‌انتخاب[73]  مي‌باشد. اين روش از فاصله نسلي نيز استفاده مي‌كند. به هر حال، در روش  پيشانتخاب ، افراد مستعد تعويض و به طور تصادفي معلوم نمي‌شوند، بلكه اين يكي از والدين است (آنكه برازندگي كمتري دارد) كه هدف تعويض قرار مي‌گيرد.

معكوس‌گرايي[74]  - تا به حال، تنها دو اپراتور بازتوليد و قطع براي توليد نسل جديد بحث شده‌اند. گروه سوم اپراتورها شامل اپراتورهاي بازترتيب[75] مي‌باشد.

اپراتورهاي بازترتيب، ترتيب بيتي يا كاراكتري را در يك استرينگ يا كروموزوم را به هم مي‌زنند. به طور اساسي، دو نوع اُپراتور بازترتيبي وجود دارد. آنهايي كه محل و موقعيت بيت يا كاراكتر را عوض مي‌كنند و ديگري آنهايي كه مقدار اَلل را عوض مي‌كنند.

معكوس‌گيري، متداول‌ترين اُپراتوريست كه محل بيت يا كاراكتر را عوض مي‌كند. دو نقطه از كروموزوم انتخاب مي‌شود و سپس در آن محل، كروموزوم بريده ويا قطع مي‌شود. قسمتي كه بين اين دو نقطه قرار گرفته، معكوس شده و سپس كروموزوم دوباره سر هم مي‌شود. به طور مثال، كروموزم نمونه زير را در نظر بگيريد. نقاط قطع را بين اَلل دوم و سوم و ديگري بين ششم و هفتم در نظر بگيريد.

 ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 

با عمل معكوس‌گيري ، كروموزوم مربوطه به شكل زير در مي‌آيد:

ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM

 

در نگاه اول، اين پروسه چندان دلچسب به نظر نمي‌رسد ولي براي برخي مواقع بسيار موثر مي‌باشد. مثلا فرض كنيد يك الگوي بسيار برازنده داريم كه داراي دو محل فيكس ولي دور از هم مي‌باشد. اين الگو (يا كروموزوم هاي متعلق به مجموعه اين الگو) در معرض حذف توسط اُپراتور قطع خواهند بود. با عمل معكوس‌گيري اين دو نقطه فيكس و دور از هم به همديگر نزديك مي‌شوند. البته در تركيب با اپراتور قطع مساله از نظر پياده‌سازي كمي مشكل‌تر مي‌شود چراكه معكوس‌گيري فقط براي برخي افراد نسل و نه همه جمعيت اعمال مي‌شود.

جايگشت[76]  -  اپراتورهاي بازترتيبي زيادي وجود دارند كه مقادير اَلل ها را عوض مي‌كنند. اين نوع اُپراتورها معمولا هنگامي كه نياز به جايگشت يك استرينگ (كروموزوم) براي رسيدن به جواب مساله باشد، مطرح مي‌شوند. به طور مثال مساله فروشنده دوره گرد[77]  را در نظر بگيريد. در اين مساله دنبال كوتاه‌ترين مسير بسته هستيم كه اولا فروشنده همه شهرها را ويزيت كند و ثانياً هر شهر فقط يك‌بار ويزيت شود. اگر به هر شهر يك شماره اختصاص دهيم، آنگاه يك جواب ممكن[78]  يك استرينگ خواهد بود كه شماره شهر نشانگر ويزيت آن شهر و ترتيب ظهور يا حضور كد شهر در استرينگ مربوطه نشان‌دهنده ترتيب ويزيت شهرها مي‌باشد. حال هر تغييري در جايگشت استرينگ بدهيم، به هر حال استرينگ تغييريافته يك جواب ممكنست و ويزيت فقط يكبار هر شهر تضمين شده است. به هر حال ، اپراتور قطع نمي تواند جايگشت ايده‌آل را تضمين كند، فلذا اپراتور آلترناتيوي به نام اپراتور قطع شبه غالب[79]  وجود دارد كه شانس كروموزوم جديدالولاده را از نظر شباهت (جايگشتي) به والدينش بيشتر مي‌كند. براي استفاده از اين اپراتور، بايد پس از انتخاب والدين، دو نقطه قطع روي آنها انتخاب كرد. سپس زير استرينگ‌هاي بين دو نقطه هر والد را بر مي‌داريم و با همديگر عوض مي‌كنيم. حال براي حفظ جايگشت مقادير عوض شده را مجددا بازتركيب مي‌كنيم. با يك مثال قضيه روشن‌تر مي‌شود:

دو والد 8 كاراكتري زير را در نظر بگيريد كه براي سهولت اَلل هاي غيرتكراري دارند. دو نقطه قطع براي هر والد،  طوري انتخاب مي‌كنيم كه زيراسترينگ مياني بريده شود ( يك نقطه قطع بين محل هاي سوم و چهارم و نقطه ديگر بين محل هاي پنجم و ششم ).

 

8

6

4

2

1

3

5

7

: والد1

8

4

7

3

6

2

5

1

: والد2

 

از محل قطع، زيراسترينگ‌ها را بريده و تعويض مي‌كنيم (كاراكترهاي عوض‌شده، پررنگ نمايش داده شده‌اند) :

 

8

7

6

5

4

3

2

1

محل

8

6

4

3

6

3

5

7

: والد1

8

4

7

2

1

2

5

1

: والد2

 

 حالا والد 1، دو تا 6 و دو تا 3 دارد همانطور كه والد 2، دو تا 1 و دو تا 2 دارد. حالا چون 6 جديد جايگزين با 1 ( در واحد 1، قبل از عمل قطع و جايگزيني ) شده‌است، براي حفظ جايگشت بايد 6 قديمي ( در محل هفتم ) با مقدار 1 (تعدادي كه جايگزيني براي آن اتفاق افتاده‌است ) عوض شود. همين كار را براي 3 جديد نيز انجام مي‌دهيم وسپس همين كار را براي والد 2 نيز انجام مي‌دهيم‌، نهايتا دو والد قطع‌داده شده با حفظ جايگشت را به صورت زير خواهيم داشت. بايد دقت شود كه آلان هر دو والد هنوز اَلل غير تكراري دارند و فقط جايگشت رخ داده است .

 

8

7

6

5

4

3

2

1

محل

8

1

4

3

6

2

5

7

: والد1

8

4

7

2

1

3

5

6

: والد2

  

اپراتور PMX تنها اپراتور جايگشتي نيست، بلكه اپراتورهايي مثل قطع ترتيبي[80]  و قطع سيكلي[81]  نيز وجود دارند. اپراتور OX بسيار شبيه PMX است ولي در نحوه حذف مقادير تكراري، متفاوت است.

بهینه یابی چند متغیره –  مسائل عملی بر خلاف مثال انگیزشی یاد شده، نوعا دارای بیش از یک متغیر مستقل (متغیر تصمیم‌گیری) می‌باشند. لذا باید به ترتیب حضور یا تاثیر سایر متغیرها را در نظر گرفت. در نظر اول، ممکن است به جای تعریف یک کروموزم، با چند کروموزم کار کنیم ولی آنچه که متداول است، چسباندن همه کروموزوم ها برای تشکیل یک استرینگ طولانی و سپس استفاده از الگوریتم GA تک کروموزومی می باشد.

بهینه یابی مالتی آبجکتیو[82] - این نوع مسائل دارای چند تابع هدف هستند که باید همزمان اپتیمم شود.  یکی از روش ها ایجاد سازگاری برای داشتن چند تابع برازندگی، جهت استفاده از GA برای مسائل چند هدفی، رتبه‌بندی افراد و بهره‌گیری از مفهوم غالب یا سلطان[83] می‌باشد. با مرتب‌کردن افراد (کروموزوم ها) به ترتیب نزولی یا صعودی، آنگاه پروسه انتخاب از روی لیست مرتب‌شده کروموزوم‌ها صورت می‌گیرد.

قالب بندی[84] - در برخی مسائل، مقدار برازندگی به مفهوم مطلق آن ممکنست روی همگرایی یا عملکرد الگوریتم GA تاثیر بسزائی داشته باشد. به عبارتی، اگر برازندگی یک کروموزوم در یک جمعیت نمونه بین 0.5 تا 1.0 تغییر کند، آنگاه ممکنست نتایجی متفاوت با سیستمی بگیریم که برازندگی همان کروموزوم بین 99.5 تا 100.0 تغییر می‌کند. یک راه کاهش این تاثیر، قالب‌بندی بدین معنیست که از مقادیر برازندگی به یک اندازه کم کنیم، به طوریکه کمترین برازندگی همیشه یک سطح استاندارد داشته باشد.

رتبه‌بندی[85] یا نرمالیزاسیون خطی[86]- در این روش که به منظور کاهش تاثیر مقدار برازندگی روی نتایج می‌باشد، برازندگی‌ها ابتدائا به ترتیب نزولی مرتب می‌شوند. سپس با استفاده ازمقادیر ما’زیمم و مینیمم برازندگی، اطلاعات برازندگی نرمالیزه می‌شوند.

مفهوم دیپلوئید و هاپلوئید -  کروموزوم‌هایی که در هر محل از استرینگ می‌توانند دو اَلل داشته باشند موسوم به دیپلوئید هستند. یکی از اَلل ها همیشه غالب است و فنوتایپ مربوطه فقط تحت تأثیر اَلل غالب می‌باشد. شایان ذکر است که در برخی از حالات یا زمان‌ها، اَلل غیرغالب می‌تواند مسلط شده و اَلل غالب شود. به عبارتی، دیپلوئیدها همیشه دارای اَلل های غیرغالب و کمون هستند تا در آینده احتمال فعال‌شدن آنها وجود داشته باشد. در طبیعت نیز همینطورست، ممکنست یک فنوتایپ کاملا برازنده یا سازگار باشد ولی اگر محیط پیرامون تغییر خصوصیت دهد، آنگاه این سوپرکروموزوم به یک کروموزوم عادی تنزل کند. نقطه مقابل کروموزوم دیپلوئید، مفهوم کروموزوم هاپلوئید است که دارای قابلیت سازگاری یا تطبیقی ساختاری نمی‌باشد.

روش های ترکیبی[87] - مسائلی در عمل وجود دارند که روش بهینه بهینه‌یابی (!) آنها، شامل ترکیب دو روش GA و یک روش جستجوی کلاسیک می‌باشد. روش براین ایده استوارست که اگر یک جستجوی کلاسیک خیلی قوی در دست داریم ولی حساس به حدس اولیه است، آنگاه می‌توان با GA به نزدیکی‌های منطقه اکسترمم محلی رفت و سپس به روش کلاسیک(سنتی) برای جستجوی سریعتر و دقیق‌تر، سوئیچ نمود.

شایان ذکرست که اصطلاح ترکیبی به روش‌هایی که دقیقا مثل GA ارائه شده توسط هُلند نیستند نیز اطلاق می‌شود. به طور مثال روش‌هایی وجود دارند که کروموزوم می‌تواند دارای اَلل های غیرباینری نیز باشد، مثلا یک عدد حقیقی باشند. بدیهیست که اُپراتورهایی نظیر جهش یا قطع باید متناظرا و مقتضیا عوض شوند.

الگوریتم های ژنتیک با دانش افزوده[88] - در برخی مسائل خاص، می‌توان اُپراتورها را به‌نحوی بهبود داد که نه تنها از اطلاعات برازندگی کروموزوم‌ها استفاده کنند، بلکه از اطلاعات مسئله مثل قیود عملی یا روابط طبیعی نظیر بیلان جرم و انرژی نیز بهره ببرند. در این صورت الگوریتم GA خیلی هم کورکورانه عمل نمی‌کند، بلکه حضور یا استفاده از اپراتورهای با دانش افزوده به نوعی به حل سریع‌تر کمک کرده یا به خود الگوریتم به ویژه قسمت انتخاب کروموزوم‌ها برای تولد افراد نسل جدید خط می‌دهند.

الگوریتم های ژنتیک پرورشی[89] - در این نوع روش‌ها، درست شبیه جوجه‌کشی یا پرورش گاوهای شیرده، هر کروموزوم عادی برای تناسل یا تولید جمعیت انتخاب نمی‌شود، بلکه کروموزوم‌های خاصی مثلا آنهایی که دارای برازندگی بالا هستند کاندیدای والد برای تولید نسل بهتر، انتخاب می‌شوند. معمولا اپراتور قطع بکار گرفته شده، یک اپراتور کاملا تصادفی می‌باشد.

روش های نوترکیبی تصادفی[90] - در این روش کروموزوم فرزند به این صورت تولید می‌شود که ابتدا اَلل‌های مشترک بین والدین درج می‌شوند و سپس اَلل‌های باقیمانده به طور تصادفی مقداردهی می‌شوند. به تجربه ثابت شده است که این روش برای برخی مسائل، بسیار عالی کار می‌کند.

تنوع در اپراتور قطع -  یکی از اپراتورهایی که خیلی تحت مطالعه و تحقیق قرار گرفته است، اپراتور قطع می‌باشد. به طور مثال اپراتورهایی که به جای قطع و تکه‌تکه شدن در دو نقطه، در سه نقطه یا بیشتر[91]  عمل قطع انجام می‌شود. عینا ممکن است عمل قطع(ولو در دو نقطه) برای بیش از دو والد رخ دهد، یعنی اپراتورهای قطع چند والدی[92] نیز داریم. اپراتور قطع یکنواخت[93]، به اینصورت عمل می‌کند که دو والد یک فرزند تولید می‌کنند ولی برای اَلل‌های فرزند، هر دفعه یک والد بطور رندام انتخاب می‌شود و اَلل متناظر از همان محل از والد به فرزند کپی می‌شود.

اپراتور نیم یکنواخت[94] مثل اپراتور یکنواخت است ولی با این تفاوت که بعد از اتمام عمل قطع، هر کدام از فرزندان مجددا تحت عمل قطع یکنواخت(UX) قرار می‌گیرند تا فرزندان به والدین شبیه‌تر باشند.

 

 الگوریتم‌های ژنتیک موازی

از آنجاییکه الگوریتم‌های ژنتیک، حل‌های ممکن یا آلترناتیو را پردازش می‌کند ، لذا می‌توان نوعی توازی و یا پردازش موازی برای آن متصور شد. باید دقت نمود که این خصیصه ذاتی الگوریتم است وگرنه الزاماً آسانی و سهولت در پیاده‌سازی موازی آن ندارد. اگر الگوریتم ژنتیک ولو بخواهد روی یک سیستم چند پروسسوری یا حتی پارالل کار کند، آنگاه نیازمند نوعی بهبود در الگوریتم ژنتیک هستیم، چرا که مثلاً برای تولید نسل جدید هنگام پردازش کروموزوم‌ها اعم از انتخاب، عمل قطع و یا استفاده از سایر پارامترها، می‌بایست به همه افراد جمعیت حاضر دسترسی داشته‌باشیم و این با موازی‌سازی همخوانی ندارد.

در قاموس توازی‌سازی[95] ، کار کردن با یک مدل همه‌شمول ، بسیار سخت است. به عبارتی اگر با سیستمی سروکار داریم که همه افراد، عناصر یا آبجکتهای آن از همدیگر تاثیر بپذیرند،آنگاه موازی‌سازی آن غیر ممکنست، مگر اینکه به نوعی با یک نگرش یا مدل دیگری که لااقل به طور گروهی و نه انفرادی، مجموعه مورد نظررا ببیند، کار کنیم.

تغییر یا تعویض مدل جمعیتی در الگوریتم های ژنتیک ، رویکردهای متفاوتی دارد. از اینرو، شاخه جدیدی در پیاده سازی موازی الگوریتم ﮋنتیک مطرح شده که در نوع خود ابتکاری و جالب می باشد.

این انشعاب جدید، موسوم به الگوریتم های ﮋنتیک موازی ( PGAS ) است که در ادامه به دو مدل معروف آنها، یعنی مدل مجمع‌الجزایری و مدل سلولی پرداخته می‌شود.

مدل مجمع‌الجزایری -  مدل مجمع‌الجزایری یا مدل دانه درشت‌ها، با چند جمعیت همه‌شمول، یا چند گروه جمعیتی که هر کدام با الگوریتم های GA   در حال اجرا شدن هستند، کار می‌کند. به عبارتی هر پروسسور یک جمعیت را پیش می‌برد یا متکامل می‌کند. ارتباط این جمعیت‌ها با همدیگر مطابق مفهوم مهاجرت[96] انجام می‌شود. نحوه مهاجرت کروموزوم‌ها از جمعیتی به جمعیت دیگر نیز تنوع خاص خودش را دارد. در برخی مدل‌ها، مهاجرت تصادفیست و در برخی دیگر درصد مهاجرت مقدار ثابتی می‌باشد. در بعضی دیگر مهاجرت‌ها همزمان و در مدل‌های دیگر ممکنست مهاجرت‌ها غیرهمزمان باشد. مسیردهی مهاجرت‌ها هم مهم است، ممکنست جمعیت مقصد یا مبدا بطور تصادفی انتخاب شود و ممکن است در قالب یک سیکل بسته باشد یا اینکه بطور طبیعی، مهاجرت فقط بین همسایه‌ها[97]  رخ دهد!   

نکته جالب این مدل، دخیل کردن مفهوم «رفاه»[98]  است. بدین معنی که چون هر پروسسور جمعیت خود را متکامل می‌کند، آنگاه هر کدام ممکنست به جوابهای مختلفی همگرا شوند، لذا هنگام کند شدن همگرایی ممکنست جمعیتهای با برازندگی متوسط بالاتر، مهاجرپذیرتر شوند! این مفهوم مهاجرپذیری یا وجود جمعیت‌های مترفه‌تر، بسیار مناسب مسایل مولتی‌مودال (وجود چندین اپتیمم محلی) می‌باشد. از نظر عملی نیز، مدل مجمع الجزایری دارای گروه خون O+  می باشد، چون دهنده خوبی است !!!

مدل مجمع‌الجزایری، فقط با انتقال یا مهاجرت اطلاعات محدود معدودی بین پروسسورها ( جمعیتها ) کار می‌کند، لذا برای بسیاری از معماری‌های سخت‌افزاری/ نرم‌افزاری قابل کاربرد است، نظیر شبکه کامپیوترها، سیستم‌های توزیع‌شده، ماشین های چند دستوری – چند داده‌ای[99] و شبکه های اینترنتی.

مدل سلولی – این نوع مدل سازی که به مدل دانه ریز[100]  یا نفوذ[101] می‌باشد از قید ومحدودیت فضایی برای کروموزوم‌ها ( و نه جمعیت ) استفاده می‌کند. قید و محدودیت مربوطه معروف به شبکه[102]  می‌باشد. بطور مثال در یک شبکه دوبُعدی، کروموزوم‌ها در یک آرایش ماتریسی قرار می‌گیرند. آنگاه کروموزوم‌ها یا  فقط با هم جفت می شوند که از یک ناحیه با شعاع از پیش تعیین شده ای انتخاب شده باشند.

اگر در شبکه دوبُعدی ، بطور مثال شعاع واحد را برای قید انتخاب کروموزوم‌ها تعریف کنیم، آنگاه با یک زیرجمعیت یا خانواده[103]  9 نفری مواجه هستیم، چون شعاع واحد می‌گوید برای یک کروموزوم نمونه، همسایه‌های اطراف را به اندازه یک کروموزوم جهت تشکیل زیرجمعیت انتخاب کنیم.

اگر شبکه مزبور، سه‌بُعدی یاشد، تعداد اعضاء زیرجمعیت‌ها ( جهت پردازش موازی) ، معادل 27 نفر ( کروموزوم ) می‌شود. خانواده‌ها می‌توانند با همدیگر همپوشانی داشته باشند و لذا جوابهای ممکن، بتدریج در شبکه پخش می‌شوند. بدین ترتیب بعد از مدتی نواحی مختلف شبکه، بطور پراکنده به جواب های اپتیمم می‌رسند و در نتیجه این مدل نیز علاوه بر استعداد توازی‌سازی، مناسب مسائل بهینه‌یابی مولتی‌مودال هستند ولی از نظر پیاده‌سازی‌، مناسب برای پردازش در ماشین‌های تک دستوری – چند داده‌ای هستند.

 

طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری

 

 

چکیده:

 امروزه الگوریتم‌ ژنتیک یکی از روشهای متاهیورستیک بسیار رایج در حل مسائل بهینه سازی ترکیبی به شمار می­رود. این الگوریتم فرایند تکامل تدریجی در طبیعت را بوسیله ترکیبی از الگوهای مختلف انتخاب، پیوند، جهش و جایگزینی شبیه سازی می­کند. بدین منظور برای هر یک از این الگوها اپراتور/اپراتورهایی تعریف می­گردد که پردازش آنها به پارامترهای زیادی نظیر احتمال پیوند، احتمال جهش و ... وابسته می باشد. آنچه روشن است اینکه ترکیبات مختلف این الگوها و پارامترها، الگوریتم را به جوابهای متفاوتی از هر دو جنبه کیفیت جواب و زمان همگرایی سوق می­دهند. از اینرو داشتن یک الگوریتم ژنتیک کارا به طراحی اپراتورهای مختلف، انتخاب بهترین ترکیب از بین آنها و یافتن مقادیر مناسب برای پارامترها وابسته است. این مقاله ابتدا به شناساندن برخی الگوهای رایج در اجزاء سازنده این الگوریتم پرداخته و سپس تلاش در شناساندن رویکردی مبتنی بر طراحی آزمایشات و روش شناسی سطح پاسخ برای شناخت بهترین ترکیب الگوها و نيز کشف نقاط بهینه عملکردی پارامترهای الگوریتم دارد. در پايان یک الگوریتم ژنتیک با رویکرد پیشنهادی مورد بهینه سازی قرار می گیرد. نتایج آماری حاصل از مقایسه عملکرد الگوریتم بهینه سازی شده با الگوریتم اولیه نشان می­دهد که در سطح اطمینان 95% جوابهای بهتری یافت شده است.

 

  1. مقدمه و شرح موضوع

 

الگوریتم ژنتیک یکی از رایج­ترین رویکردهای پیشنهادی در حل مسائل بهینه سازی بوده که از نظریه تکامل تدریجی الهام گرفته شده است. در این الگوریتم ابتدا بسته به نوع متغیرهای مسئله با یکی از روش­های موجود آنها را کد­گذاری می­کنند. هر رشته از متغیرهای کدگذاری شده (ژن) فرزند نام دارد که شایستگی آن با معیاری بنام تطابق که از تابع هدف مسئله بدست می­آید سنجیده می­شود. این الگوریتم با جمعیتی از فرزندان اولیه بعنوان نسل اول کار خود را شروع کرده و تولید نسل­های جدید را از پیوند افراد نسل­های پیشین انجام می­دهد. بدین منظور ابتدا فرزندانی که اکنون والد خوانده می­شوند بوسیله روش­هاییانتخاب می­شوند تا از ترکیب آنها بوسیله اپراتور پیوند و جهش فرزندان جدید تولید شوند. در این مرحله فرزندان تولید شده بوسیله یکی از روش­های موجود انتخاب شده تا نسل جدید را تشکیل دهند. نسل­های جدید معمولا از تطابق بیشتری برخوردار می­باشند و این روند تا تکامل الگوریتم ژنتیک که بوسیله یک شرط توقف بررسی می­شود ادامه می­یابد.  تا­کنون پژوهشگران زیادی به بهینه سازی الگوریتم ژنتیک پرداخته­اند که اغلب این پژوهش­ها با تنظیم مقدار پارامترهای الگوریتم سروکار داشته­اند. از آنجاییکه کارایی الگوریتم ژنتیک به انتخاب بهترین رویکردهای موجود در ساخت اجزا آن نیز بسیار وابسته بوده و این مقوله کمتر مورد توجه پژوهشگران قرار گرفته است در این نوشته به آن پرداخته می­شود. با توجه به گفته­های بالا، به نظر می­رسد در طراحی یک الگوریتم ژنتیک کارا سه مرحله بایستی پیموده شود:

  • طراحی استراتژی­های متفاوت برای ساخت الگوریتم
  • تعیین بهترین ترکیب از بین استراتژی­های طرح شده
  • تنظیم پارامترهای ترکیب بهینه استراتژی­ها

در ادامه این تحقیق ابتدا به بررسی سه مرحله بالا پرداخته و سپس این رویکرد سه مرحله­ای جهت بهینه­سازی یک الگوریتم ژنتیک که به منظور حل یکی از مسائل زمانبندی پروژه پیشنهاد شده است به کار گرفته می­شود.

 

  • طراحی استراتژی­های متفاوت برای ساخت الگوریتم

 

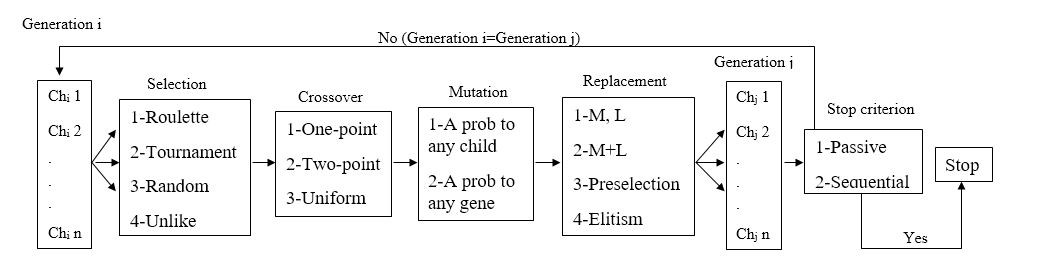
شکل زیر فرایند اجرایی الگوریتم ژنتیک و برخی از رویکرد­های رایج در ساخت آن را نشان می­دهد.

 
ژنتیک, الگوریتم ژنتیک، طراحی و تحلیل آزمایش­ها، روش شناسی رویه پاسخ, تکامل بیولوژیکی, تناظر مسائل بهینه‌سازی با پدیده انتخاب طبیعی, ترمینولوژی فرآیند تکامل بیولوژیکی, ژنتیک بیولوژیکی, اُپراتورهای ژنتيک , الگوريتم ژنتيک پايه ( Simple Genetic Algorithm-SGA ), مسأله کدينگ, مسأله قياس, نكات عملي پياده‌سازي GA, فرآيند مقياس دهي (Scaling), معكوس‌گرايي, جايگشت, الگوریتم‌های ژنتیک موازی, بهینه یابی چند متغیره , بهینه یابی مالتی آبجکتیو, مفهوم دیپلوئید و هاپلوئید, الگوریتم های ژنتیک با دانش افزوده, تنوع در اپراتور قطع , مدل مجمع‌الجزایری , مدل سلولی , طراحی بهینه الگوریتم ژنتیک با رویکردهای آماری, طراحی استراتژی­های متفاوت برای ساخت الگوریتم, شناخت بهترین ترکیب, کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه, بهینه سازی, RSM 

  • شناخت بهترین ترکیب

 

زمانیکه سیستم های مورد مطالعه تحت تاثیر چند عامل قرار دارند، طرح­های عاملی کامل­ترین طرح­ها برای مطالعه اثرات این عوامل هستند. در طراحی الگوریتم ژنتیک برای شناخت تاثیر به کارگیری الگوهای مختلف در کارایی الگوریتم، بهتر آن است که از یک طرح عاملی استفاده گردد. همچنین برای تشخیص اینکه دقیقا بین میانگین کدامیک از عامل­ها تفاوت وجود دارد می­توان آزمون کمترین تفاوت معنی­دار یا آزمون چند دامنه دانکن استفاده کرد.

 

  • تنظیم پارامترها

 

روش شناسی رویه پاسخ ترکیبی از تکنیکهای ریاضی و آمار است که هدف آن بهینه سازی پاسخ در مسائلی است که پاسخ مورد نظر تحت تاثیر چندین متغیر قرار می­گیرد. زمانیکه صورت بستگی بین پاسخ و متغیرهای مستقل نامعلوم باشد بایستی تقریبی مناسب برای بستگی واقعی موجود بین پاسخ و مجموعه متغیرهای مستقل یافت. بدین منظور می­توان از روش کمترین مربعات استفاده کرد.  پس از شناخت رویه پاسخ ، بایستی سطوحی از متغیرها را به گونه­ای که منتج به مقدار بهینه بر روی رویه پاسخ گردند، پیدا کنیم. از روش شناسی رویه پاسخ می­توان در بحث تنظیم پارامترهای الگوریتم ژنتیک بهره جست. بدین منظور می­توان از یک طرح عاملی استفاده نموده تا سطح/سطوح پاسخ تخمین زده شود. سطوح پاسخ می­تواند بصورت 1) حداقل کردن درصد انحراف نسبی جوابهای الگوریتم نسبت به جواب بهینه 2) حداقل کردن درصد انحراف نسبی زمان حل الگوریتم نسبت به زمان حل بهینه و یا هر هدف دیگری که مد نظر طراح الگوریتم باشد تعریف شود. در صورتیکه بهینه­سازی همزمان چندین هدف مد نظر قرار گیرد می­توان از روشهای بهینه­سازی چند هدفه مانند برنامه­ریزی آرمانی یا  برنامه­ریزی آرمانی فازی و یا سایر روش­های شناخته شده در این زمینه می­توان بهره برد.

 

  1. کاربرد روش پیشنهادی بر یک مسئله زمانبندی پروژه

 

در این قسمت الگوریتم ژنتیکی که برای حل مسئله سرمایه­گذاری در منابع با جریانهای نقدی تنزیل شده و روابط پیشنیازی توسعه یافته پیشنهاد داده­است جهت بینه­سازی مورد توجه قرار می­گیرد. در این الگوریتم از الگوی Tournament برای انتخاب والدین و از دو اپراتور پیوند یک نقطه­ای و یکنواخت به صورت ترکیبی استفاده شده است. همچنین از الگوی تخصیص یک احتمال جهش به هر فرزند استفاده گردیده و فرزندان تولیدی به روش Pre-selection در نسل جدید شرکت داده می­شوند. افزون بر آن هر دو معیار  Passive و Sequential به صورت ترکیبی برای توقف الگوریتم مورد استفاده قرار گرفته­اند. این الگوریتم از یک اپراتور بهبود موضعی نیز بهره جسته است. در این مقاله به منظور در دست داشتن الگوهای بیشتری جهت مقایسه، الگوهای Random و Unlike برای انتخاب والدین، تخصیص یک احتمال جهش به هر ژن برای اعمال اپراتور جهش و الگوی Elitism برای جایگزینی نیز طراحی گردید. سپس برای تشخیص بهترین ترکیب الگوها از یک طرح فاکتوریال کامل شامل 48 سطح استفاده شد که نتایج حاصل از آزمون چند دامنه دانکن برای این طرح نشان دهنده آن است که الگوریتم ژنتیکی متشکل از الگوی Unlike برای انتخاب والدین، اپراتور یکنواخت برای پیوند، تخصیص احتمال جهش به هر ژن برای اعمال اپراتور جهش، الگوی جایگزینی Pre-selection و شرط توقف Sequential به جواب­های بهتری دست یافته است. مرحله بعد تنظیم پارامترهای این ترکیب می­باشد که 5 پارامتر شامل سایز جمعیت هر نسل، احتمال انجام پیوند، احتمال انجام جهش، احتمال اعمال بهبود موضعی و تعداد نسل های متوالی برای رسیدن به شرط Sequential مورد توجه قرار گرفتند. برای تخمین تابع هدف از طرح CCF شامل طرح عاملی کسری 25-2 با 4 نقطه مرکزی و 10 نقطه محوری استفاده شد. آنگاه دو تابع هدف کمینه کردن انحراف نسبی جواب­های الگوریتم و کمینه کردن زمان حل الگوریتم تخمین زده شد که پس از حل آنها به روش برنامه ریزی آرمانی فازی مقادیر بهینه پارامترهای الگوریتم نیز شناخته شدند. در انتها برای مقایسه عملکرد الگوریتم بهینه سازی شده با الگوریتم اولیه از یک آزمون مقایسات زوجی استفاده گردید که نتایج آن نشان می­دهد در سطح اطمینان 95%  بین جواب­های دو الگوریتم تفاوت مشاهده می­شود بطوریکه این تفاوت نشان از بهتر بودن جواب­های ژنتیک بهینه­سازی شده دارد.

 

  1. نتیجه­ گیری

 

الگوریتم ژنتیک بعنوان یکی از کاراترین و موثرترین روش­های حل مسائل پیچیده بهینه­سازی ترکیبی شناخته شده و در سالهای اخیر بسیار مورد توجه پژوهشگران قرار گرفته است. نظر به استفاده فراوان از این الگوریتم، ارائه روش­هایی که پژوهشگران را به سمت  طراحی الگوریتم­هایی با عملکرد بهینه هدایت کند به عنوان یک نیاز مطرح می­باشد.  از آنجا که دیدگاههای متفاوتی در طراحی و ساخت این الگوریتم معرفی و پیشنهاد شده­اند و پارامترهای متعددی بر کیفیت جواب­های الگوریتم تاثیرگذار می­باشند، در این تحقیق روشی جهت طراحی بهینه الگوریتم­های ژنتیک پیشنهاد شد که شامل سه فاز 1)طراحی ترکیبات مختلفی از دیدگاههای رایج در ساخت الگوریتم ژنتیک، 2)انتخاب بهترین ترکیب بوسیله طراحی و تحلیل آزمایش­ها و 3)تنظیم پارامترهای الگوریتم بر روی نقاط بهینه با روش شناسی رویه پاسخ می­باشد. این رویکرد بر روی یک الگوریتم ژنتیک به طور موردی اجرا شد و مقایسات آماری نشان داد که الگوریتم ژنتیک بهینه­سازی شده عملکرد مناسب ­تری از خود بروز داده است.

از آنجا که سایر متاهیورستیک­ها نظیر الگوریتم مورچگان و شبیه سازی تبرید و ... نیز دارای دیدگاههای متفاوت ساخت و همچنین پارامترهای متعدد و موثر بر عملکرد نهایی می­باشند بنابراین می­توان از چنین رویکردی برای بهینه سازی آنها نیز بهره جست. 

 

مراجع :

[1]. R. Dawkins (1986), The Blind Watchmaker, Penguin Books, London. 

[2]. R. Dawkins (1989), The Selfish Gene , Oxford  University Press , Oxford , 2nd Edition .             

[3]. J. H. Holland (1992), Adaptation in Natural and Artificial Systems : An Introductory Analysis with Application to Biology , control and Artificial Intelligence, 2nd Edition, MIT press / Bradford Book Edition, Cambridge, Massachusetts .

[4]. D .E. Goldberg (1989), Generic Algorithms in Search, Optimization  & Machine Learning, Addison – Wesley  Publishing company Inc. 

 

 

[1] Gregur Mendel

[2] genes

[3] genetics

[4] Chromosomes

[5] Charles Darwin

[6] Origin of Species

[7] Natural Selection

[8] DeoxyriboNucleic Acid - DNA

[9] Genetic Code

[10] Allele

[11] Homozygous

[12] Heterozygous

[13] Phenotype

[14] Genotype

[15] Independent Assortment

[16] Mitosis

[17] Mutation

[18] Meiosis

[19] Gamete

[20] Haploid

[21] Diploid

[22] Homologous

[23] Kinetochore

[24] Cross-over

[25] Galapagos

[26] Population

[27] Hardy-Weinberg Law

[28] Gene Flow

[29] Genetic Draft

[30] Natural Selection

[31] John Holland

[32] Complex Adaptive Systems

[33] Genetic Operators

[34] Being

[35] Race

[36] Area

[37] Individual

[38] Gene

[39] Type

[40] Phenomenological

[41] Bit

[42] Locus

[43] Fitness Function

[44] Structure

[45] String

[46] Decode

[47] Solution Space

[48] Next Generation

[49] Reproduction

[50] Crossover

[51] Mutation

[52] Crossover point

[53] bit wise

[54] Floating point or Real numbers

[55] Resolution

[56] Rational or Fractional

[57] Mutation Rate

[58] tick

[59] Schemata

[60] Schema

[61] Similarity Template

[62] Order

[63] fixed

[64] Defining Length

[65] Occurrence

[66] Fundamental theorem of GAS

[67] Elitist selection

[68] expected value selection

[69] Replacement

[70] Crowding

[71] generation gap

[72] crowding factor

[73] preselection

[74] Inversion

[75] Reordering

[76] permutation

[77] Traveling salesman

[78] feasible

[79] Partially matched crossover- PMX

[80] Order crossover- OX

[81] Cycle crossover-CX

[82] Multi-Objective or Multi-Criteria

[83] Dominance

[84] Windowing

[85] Ranking

[86] Linear Normalization

[87] Hybrid

[88] Knowledge Augmented GAs

[89] Breeder Genetic Algorithm-BGA

[90] Random Respectful Recombination-R3

[91] Multiple Point Cross Over

[92] Multiple Parents Crossover

[93] Uniform Cross Over-UX

[94] Half-Uniform Crossover-HUX

[95] parallel  programming

[96] migration

[97] stepping - stone

[98] niching

[99] Multiple Instruction Multiple Data  -  MIMD

[100] fine-grained

[101] Diffusion

[102] grid  

[103] deme

 

 ♦♦♦ در صورت داشتن هرگونه سوال در مورد این موضوع برای ما نظر بگذارید (در پایین همین صفحه). در اسرع وقت به تمامی سوالات شما توسط کارشناس مربوطه پاسخ داده خواهد شد. با تشکر ♦♦♦

تیم ما

 مطالب تصادفی:

روش نگارش يک مقاله علمي-پژوهشي + نمونه مقاله اعتبارسنجی و ابزارسازی| نمونه مقاله توصیفی

ويژگيهاي يك گزارش نهايي تحقيق | نحوه نوشتن گزارش کار و رفرنس دهی آن

جداسازی بیولوژیک| DNA | سانتریفوژ|فیلتراسیون |تخریب سلولی| جداسازی|جذب سطحی|رسوب دهی|الکتروفورز| کریستالیزاسیون |الکتروفورز | الکترودیالیز |کروماتوگرافی

سمینار چیست؟|توضیح کامل |بررسی تفاوت همایش، کنفرانس، سمینار، کنگره، فراخوان، گردهمایی، میتینگ، جشنواره، کنوانسیون و کارگاه

پایان‌نامه چیست؟| مراحل نوشتن پایان نامه و شرح کامل آن| تخصصی

آموزش پروپوزال نویسی برای پایان نامه و رساله دکتری | تخصصی | انجام پروپوزال

مشاوره و آموزش انجام پایان نامه پروژه های تخصصی بیوتکنولوژی و مجموعه زیست سلولی

 

رشته های دانشگاهی
ژنتیک
بازدید: 26127
Rating:
( 1 Rating )
کانال تلگرامی بیوتکنولوژی و زیست شناسی اینستاگرام بیوتکنولوژی, bio1 ریسرچ گیت گوگل اسکولار بیوتکنولوژی لینکدین بیوتکنولوژی
تمام حقوق این سایت متعلق به گروه bio1 به سرپرستی پوریا غلامی تیلکو می باشد . نقل مطالب متمم بدون ذکر منبع، تخلف محسوب شده و متخلفین بر اساس قوانین جاری کشور مورد پیگرد قانونی قرار می گیرند.

جستجو